[Algorithm] 19장 너비,깊이 우선 탐색

너비, 깊이 우선 탐색(BFS, Breadth-First Search, DFS, Depth-First Search)
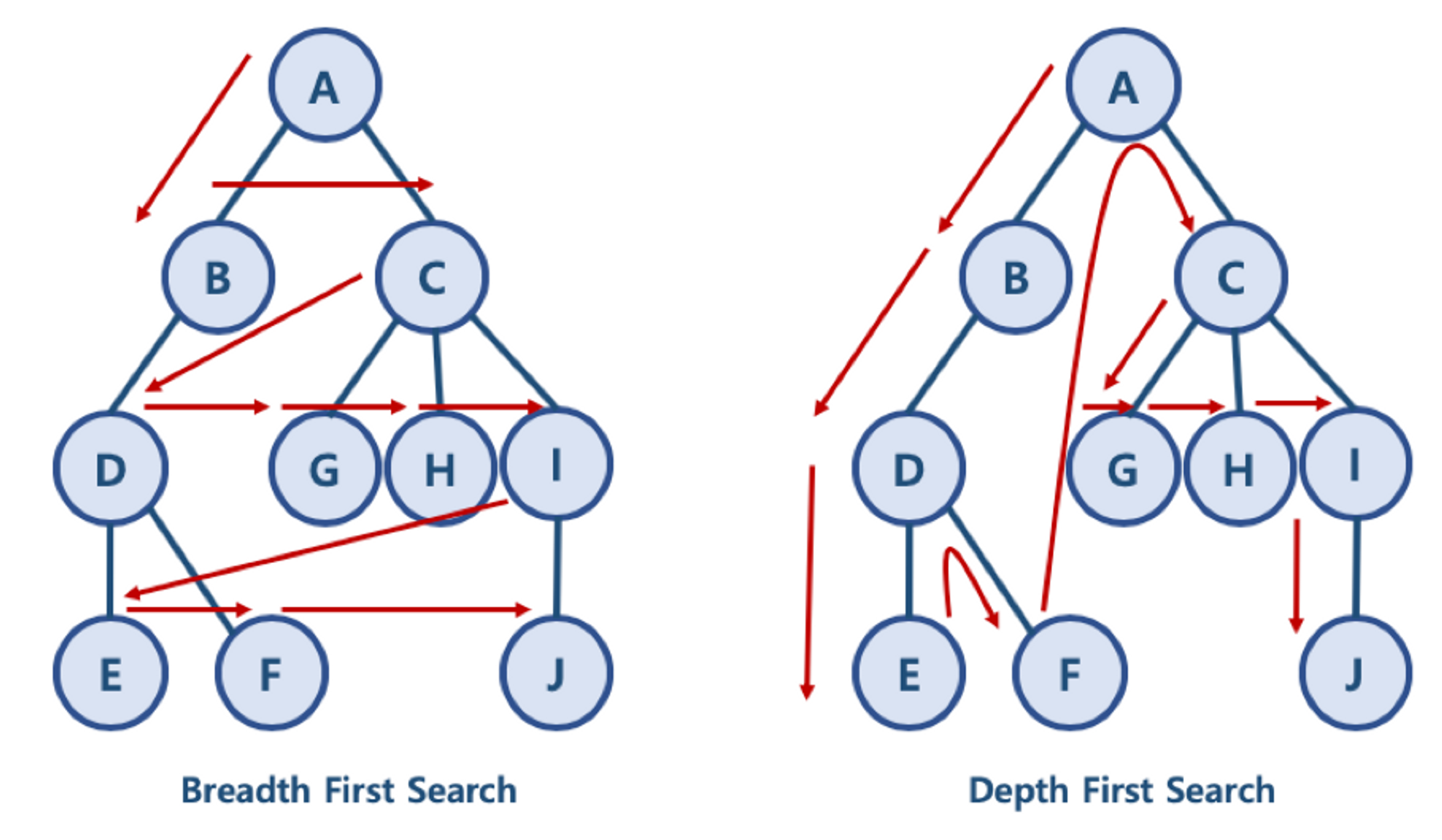
BFS와 DFS란
BFS (A - B - C - D - G - H - I - E - F - J) 한 단계씩 내려가면서, 해당 노드와 같운 레벨에 있는 노드들(형제 노드)을 먼저 순회한다.
DFS (A - B - D - E - F - C - G - H - I - J)
한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 훈회한다.
그래프를 자료구조로 작성하기
HashMap을 사용하여, 그래프를 자료구조로 작성할 수 있다.
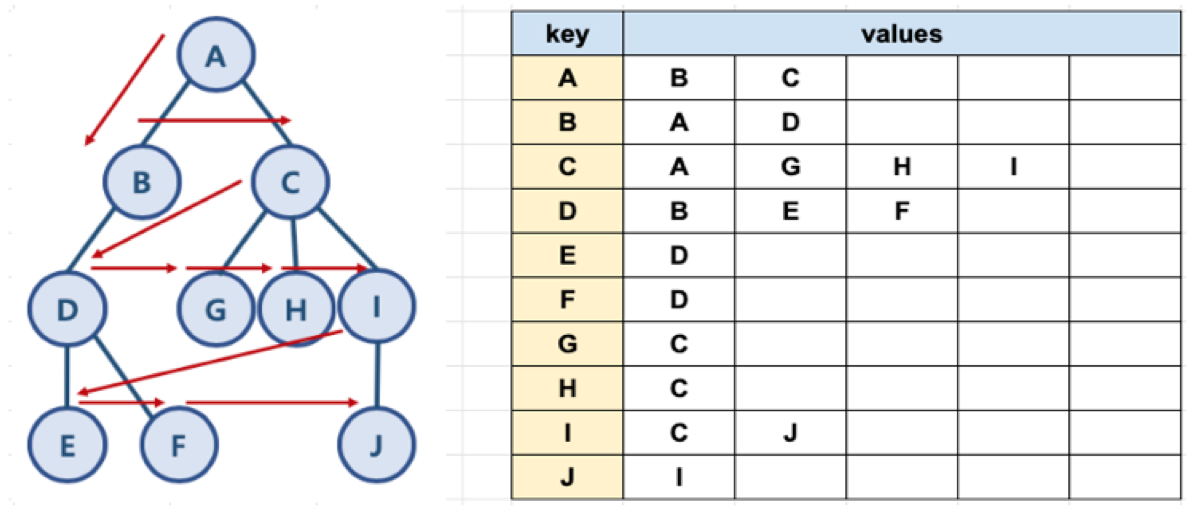
HashMap<String, ArrayList<String>> graph = new HashMap<>();
graph.put("A", new ArrayList<>(Arrays.asList("B", "C")));
graph.put("B", new ArrayList<>(Arrays.asList("A", "D")));
graph.put("C", new ArrayList<>(Arrays.asList("A", "G", "H", "I")));
graph.put("D", new ArrayList<>(Arrays.asList("B", "E", "F")));
graph.put("E", new ArrayList<>(Arrays.asList("D")));
graph.put("F", new ArrayList<>(Arrays.asList("D")));
graph.put("G", new ArrayList<>(Arrays.asList("C")));
graph.put("H", new ArrayList<>(Arrays.asList("C")));
graph.put("I", new ArrayList<>(Arrays.asList("C", "J")));
graph.put("J", new ArrayList<>(Arrays.asList("I")));
BFS 코드 구현
BFS 알고리즘은 그래프에서 가까운 노드부터 우선적으로 탐색한다는 점에서, 선입선출 방식의 큐 자료구조를 활용한다.
즉 BFS는 인접한 노드를 반복적으로 큐에 삽입하고 먼저 삽입된 노드부터 차례로 큐에서 꺼내도록 알고리즘을 작성하면 된다.
- 탐색 시작 노드 정보를 큐에 삽입하고 “방문 처리”한다.
- 큐에서 노드를 꺼내 방문하지 않은 인접 노드 정보를 모두 큐에 삽입하고 방문 처리한다.
- 2번의 가정을 더 이상 수행할 수 없을 때까지 반복한다.
방문 처리란, 탐색한 노드를 재방문하지 않도록 구분하는것이다. 큐에 한 번이라도 삽입된 노드를 다시 삽입하지 않도록 체크하는 것이다.
그래프 예시를 통해 BFS 동작 과정을 알아보겠다. 노드1을 시작 노드로 설정한다.
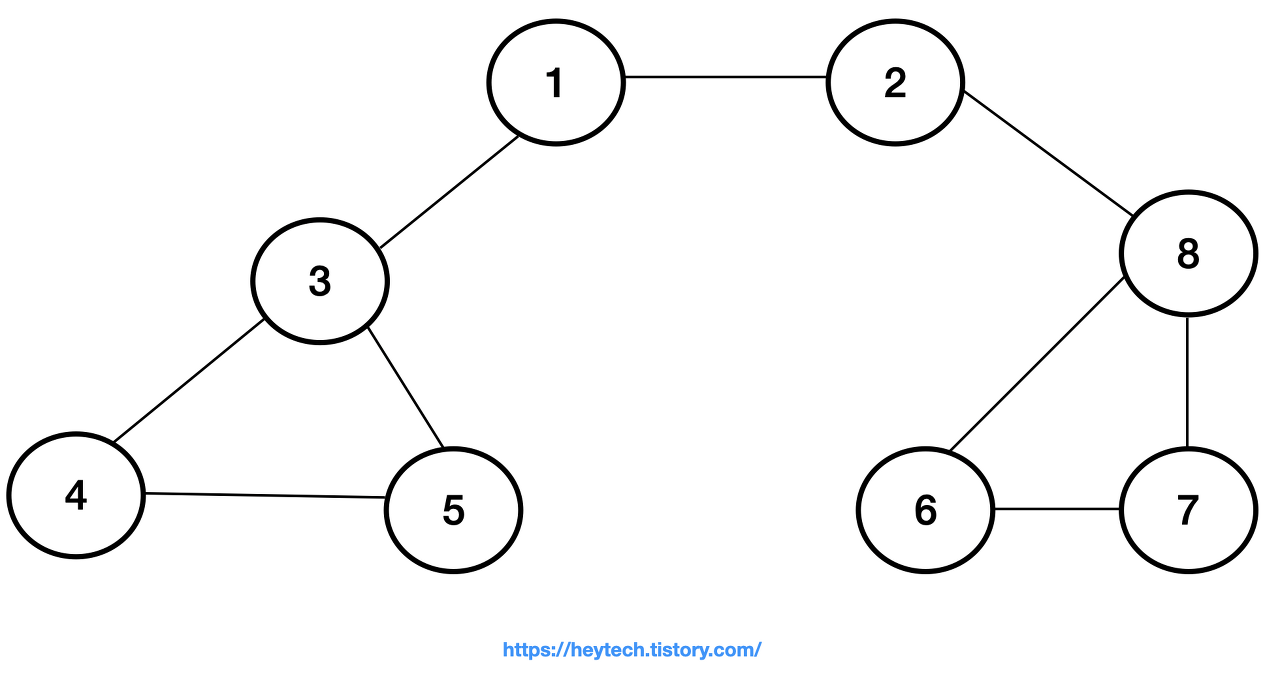
편의상 현재 큐에서 꺼내 처리 중인 노드는 파란색으로, 방문 처리한 노드는 회색으로 표시하겠다.
-
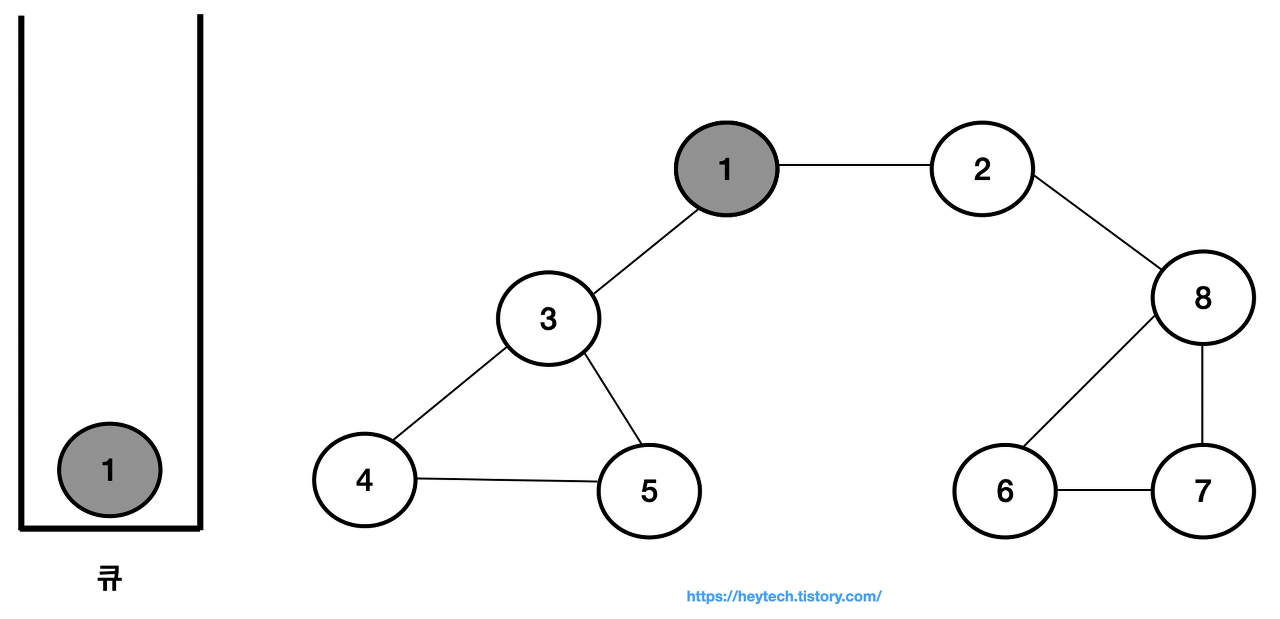
시작 노드인 노드 1을 큐에 삽입하고 방문 처리한다.
-
큐에서 노드1을 꺼내고 노드1과 인접한 노드 2,3을 큐에 삽입하고 방문 처리한다.
-
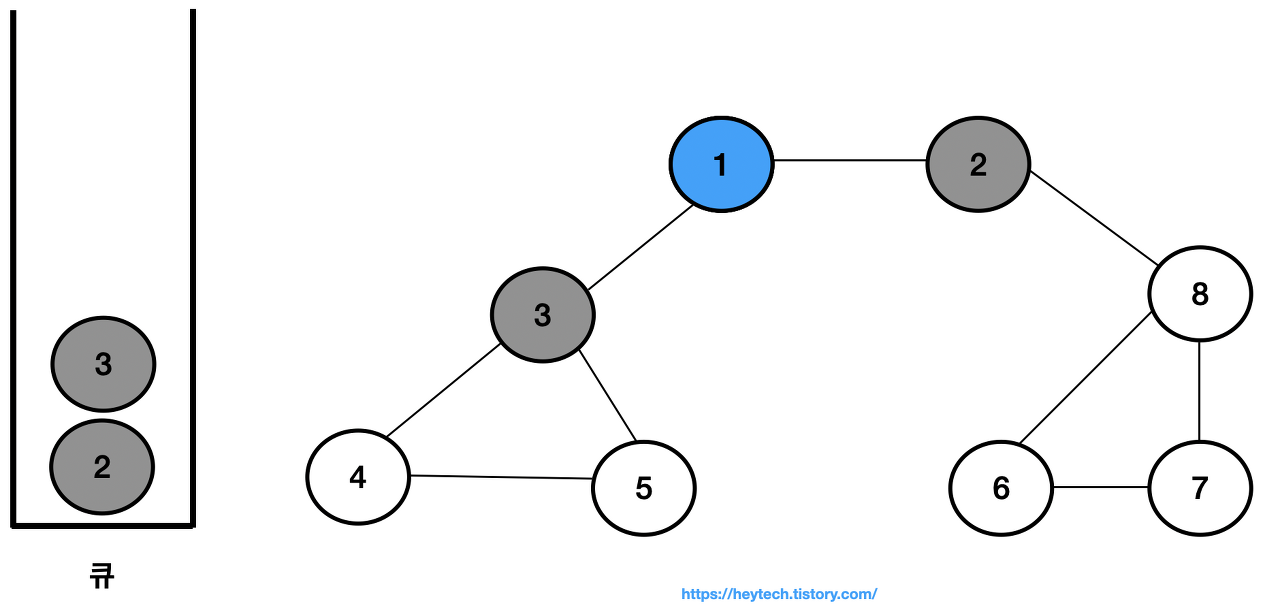
큐에서 노드 2를 꺼내고 노드 2와 인접한 노드 8을 큐에 삽입하고 방문 처리한다.
-
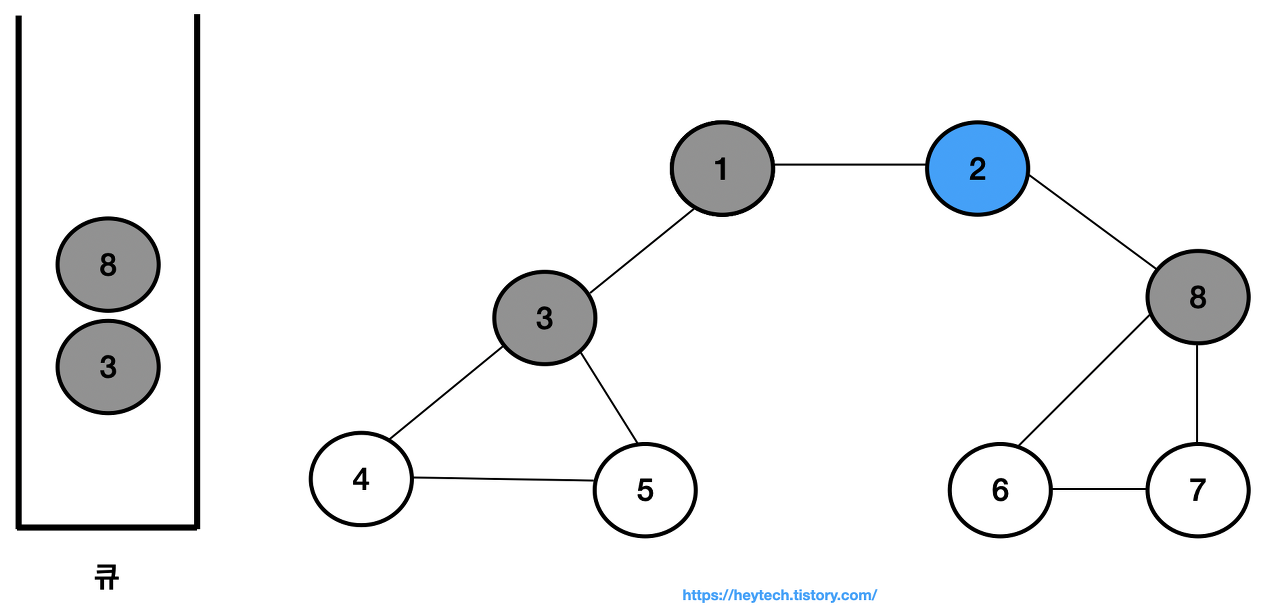
큐에서 노드 3을 꺼내고 노드 3과 인접한 노드 4,5를 큐에 삽입하고 방문 처리한다.
-
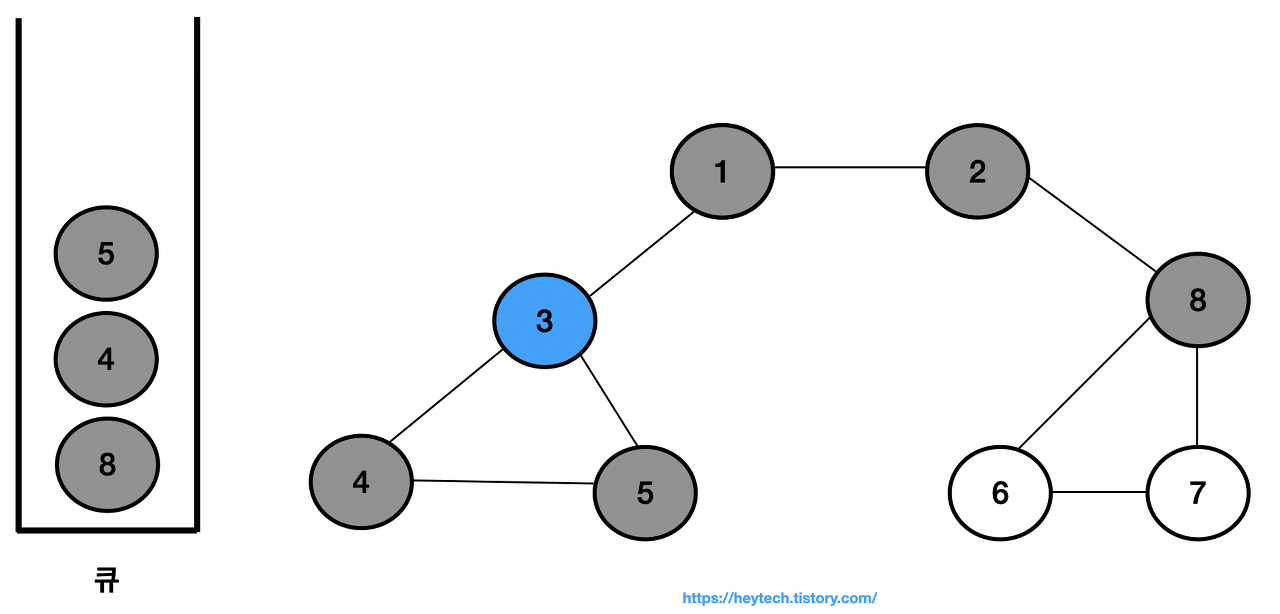
큐에서 노드 8을 꺼내고 노드 8과 인접한 노드 6,7을 큐에 삽입하고 방문 처리한다.
-
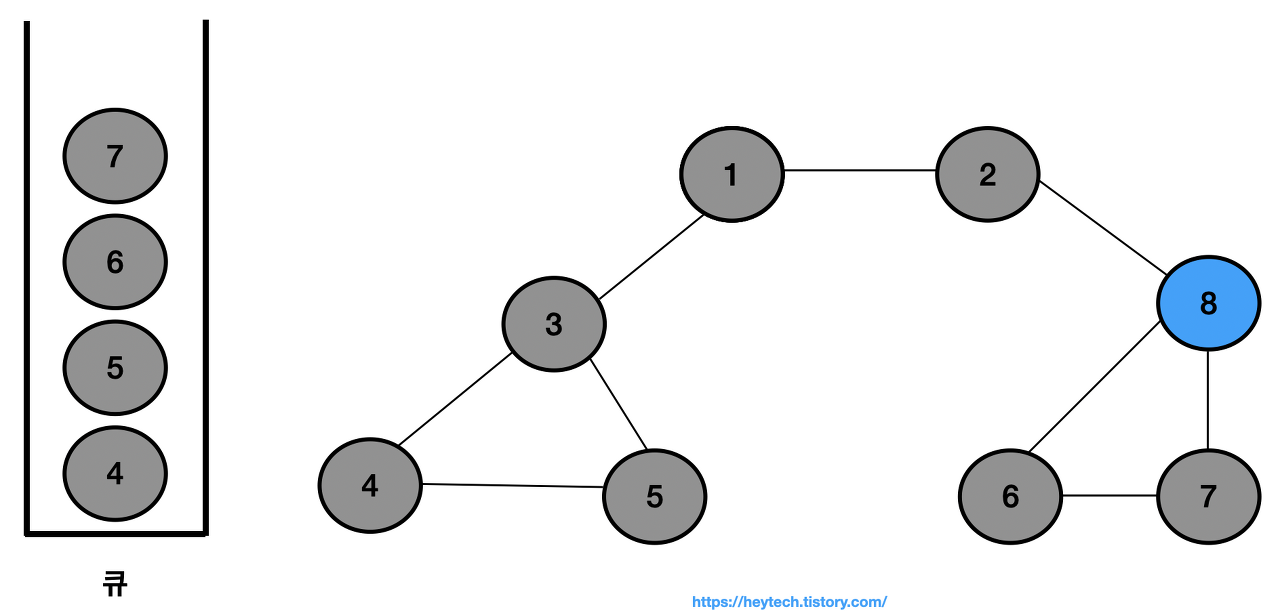
그래프 내 노드에서 방문하지 않은 노드가 없으므로 큐에서 모든 노드를 차례대로 꺼낸다.
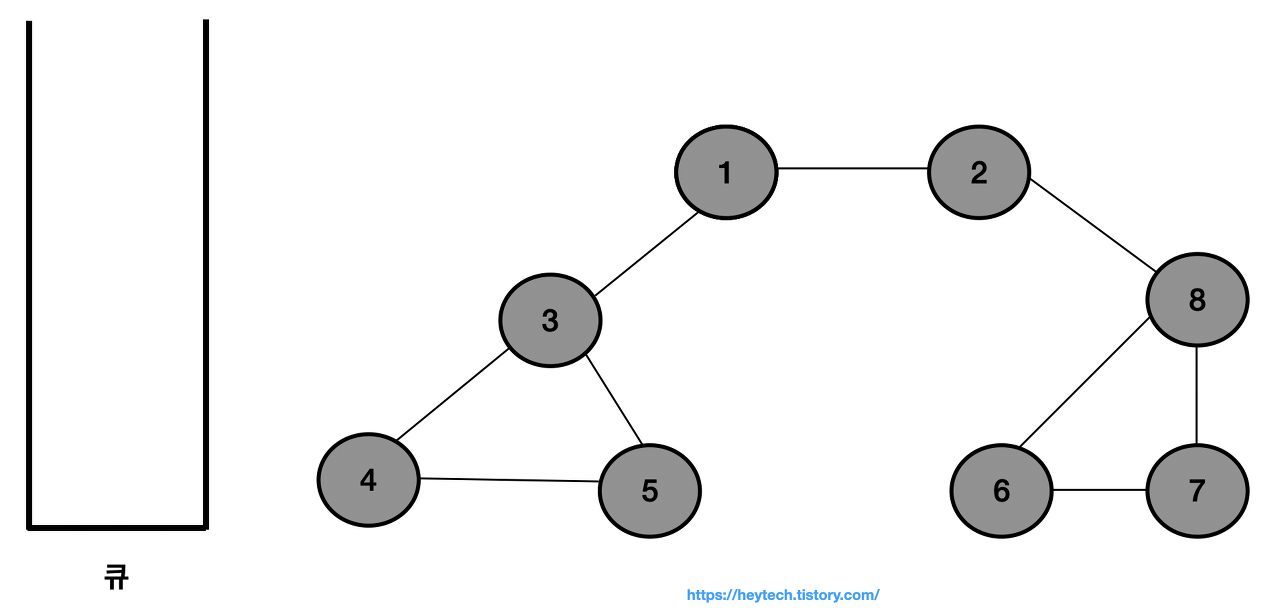
결과적으로 노드의 탐색 순서, 즉 큐에 삽입한 순서는 다음과 같다.
1 → 2 → 3 → 8 → 4 → 5 → 6 →7
public class BFSSearch {
public ArrayList<String> bfsFunc(HashMap<String,ArrayList<String>> graph, String startNode){
ArrayList<String> visited = new ArrayList<>();
ArrayList<String> needVisit = new ArrayList<>();
needVisit.add(startNode);
while (needVisit.size() > 0){
String node = needVisit.remove(0);
if (!visited.contains(node)){
visited.add(node);
needVisit.addAll(graph.get(node));
}
}
return visited;
}
public static void main(String[] args) {
HashMap<String, ArrayList<String>> graph = new HashMap<>();
graph.put("A", new ArrayList<>(Arrays.asList("B", "C")));
graph.put("B", new ArrayList<>(Arrays.asList("A", "D")));
graph.put("C", new ArrayList<>(Arrays.asList("A", "G", "H", "I")));
graph.put("D", new ArrayList<>(Arrays.asList("B", "E", "F")));
graph.put("E", new ArrayList<>(Arrays.asList("D")));
graph.put("F", new ArrayList<>(Arrays.asList("D")));
graph.put("G", new ArrayList<>(Arrays.asList("C")));
graph.put("H", new ArrayList<>(Arrays.asList("C")));
graph.put("I", new ArrayList<>(Arrays.asList("C", "J")));
graph.put("J", new ArrayList<>(Arrays.asList("I")));
BFSSearch bObject = new BFSSearch();
System.out.println(bObject.bfsFunc(graph, "A"));
}
}
복잡도
- 큐에서 Node를 넣고 빼는 데 걸리는 시간
BFS는 방문한 노드를 표시하고 다시 방문하지 않는다.
큐를 사용해 맨 뒤에 삽입하고 맨 앞에 데이터를 꺼내오는 연산들을O(1)으로 생각할 수 있다.
최대 V개의 Node들이 큐에 들어갔다 나온다. Node들이 큐에 들어갔다 나오는 데 걸리는 총 시간은 O(V)라고 할 수 있다.
- 큐에서 뺀 Node의 인접한 Node들을 도는데 걸리는 시간
큐에서 Node를 꺼낼 때마다, 그 Node에 인접한 다른 Node들을 돈다.
위에서 이야기했듯이 모든 Node는 큐에 한번만 들어가서 한번만 나올 수 있다.
Node가 한 번 나올 때마다 그 Node의 인접 리스트를 돈다. 그러니까 모든 Node들의 인접 리스트를 딱 한번만 돈다고 할 수 있다. 그럼 총 엣지 수가 E 니까 이 단계도 총 E에 비례하는 만큼 실행된다고 할 수 있다.
큐에서 뺀 Node들의 인접한 Node들을 도는데 O(E) 가 걸리는 것이다.
일반적인 BFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 시간 복잡도: O(V + E)
DFS 코드 구현
DFS 알고리즘은 선입후출 방식의 스택 자료구조를 사용한다.
- 탐색 시작 노드 정보를 스택에 입력하고 방문 처리한다.
- 스택 내 최상단 노드에 방문하지 않은 노드가 있다면 그 인접 노드 정보를 스택에 삽입하고 방문처리한다. 만일 방문하지 않은 인접 노드가 없다면 스택 내 최상단 노드를 꺼낸다.
- 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
방문 처리란, 탐색한 노드를 재방문하지 않도록 구분하는것이다. 큐에 한 번이라도 삽입된 노드를 다시 삽입하지 않도록 체크하는 것이다.
그래프 예시를 통해 DFS 동작 과정을 알아보겠다. 노드1을 시작 노드로 설정한다.
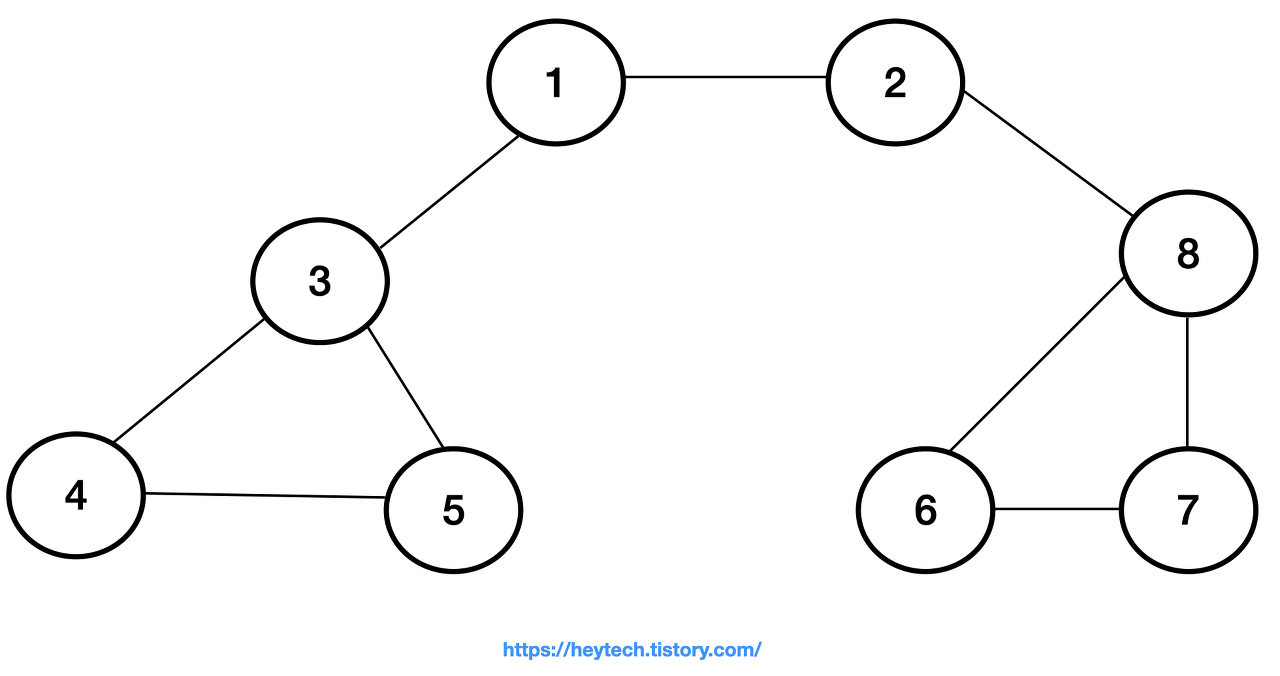
-
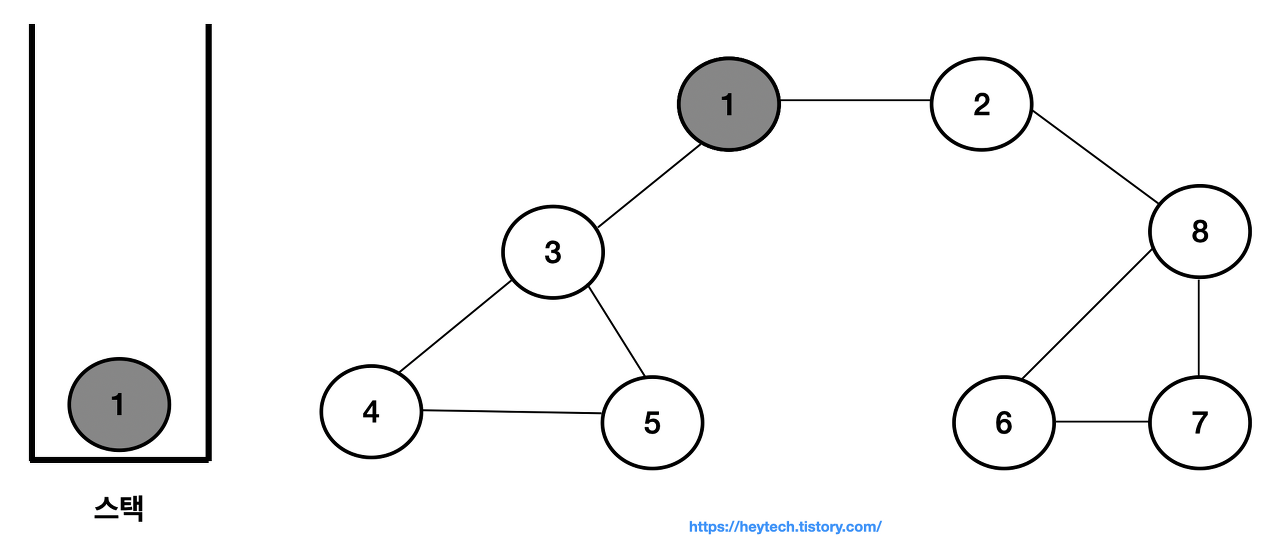
시작 노드인 노드 1을 스택에 삽입하고 방문 처리한다.
-
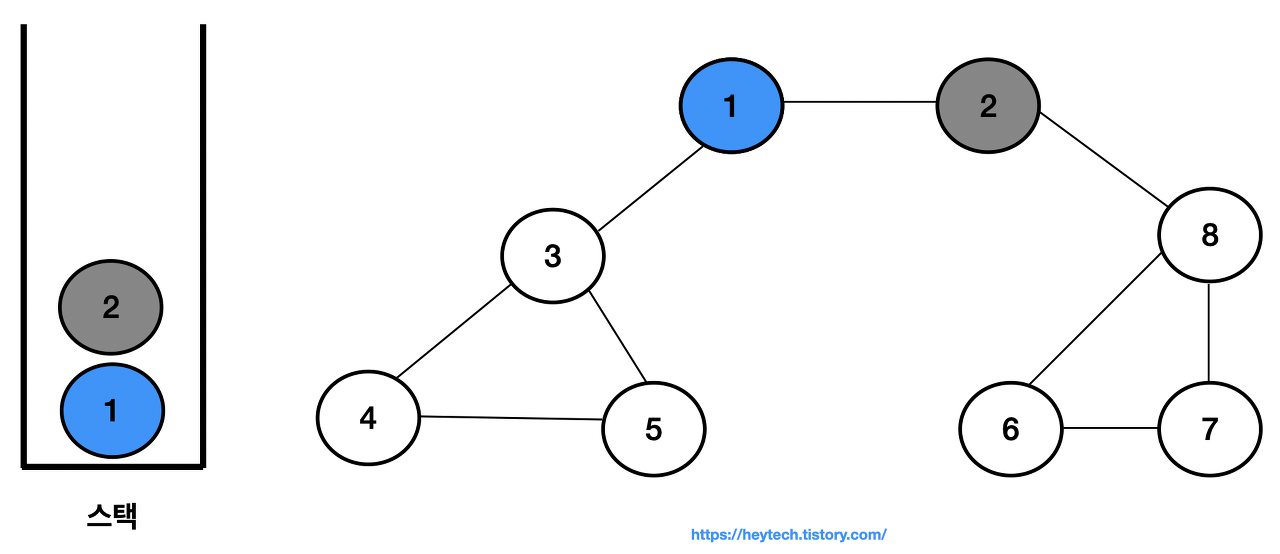
스택 내 최상단 노드인 노드 1에 인접한 노드는 2, 3이 있다. 번호가 낮은 노드 2를 스택에 삽입하고 방문 처리한다.
-
스택 내 최상단 노드인 노드 2에 인접한 노드 8을 스택에 삽입하고 방문 처리한다.
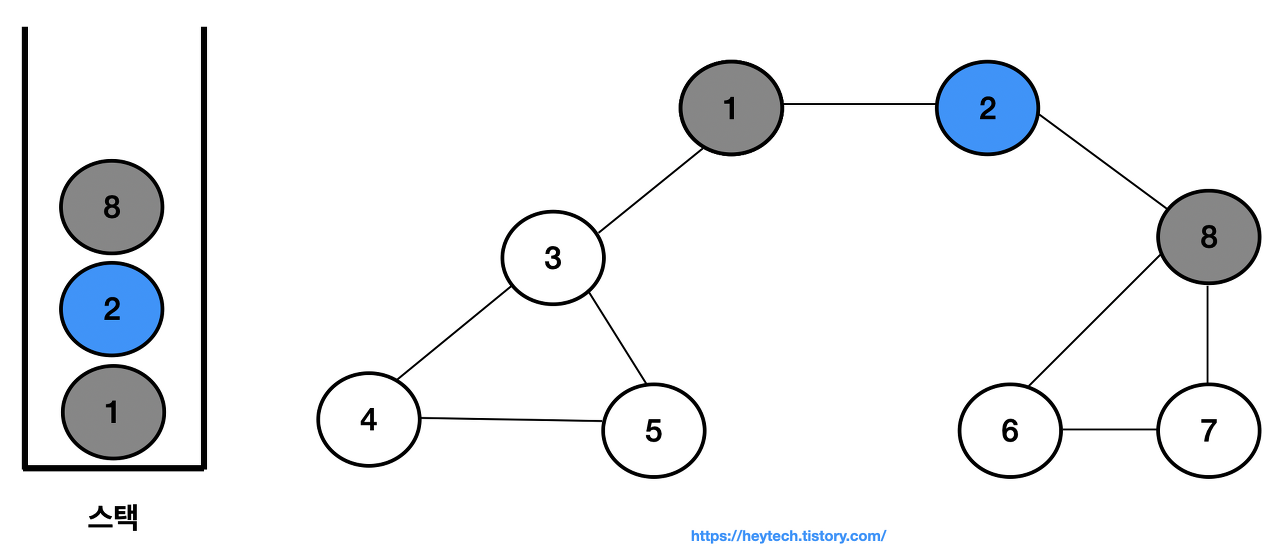
-
스택 내 최상단 노드인 노드 8에 인접한 노드는 6과 7이 있다. 번호가 낮은 노드 6을 스택에 삽입하고 방문 처리한다.
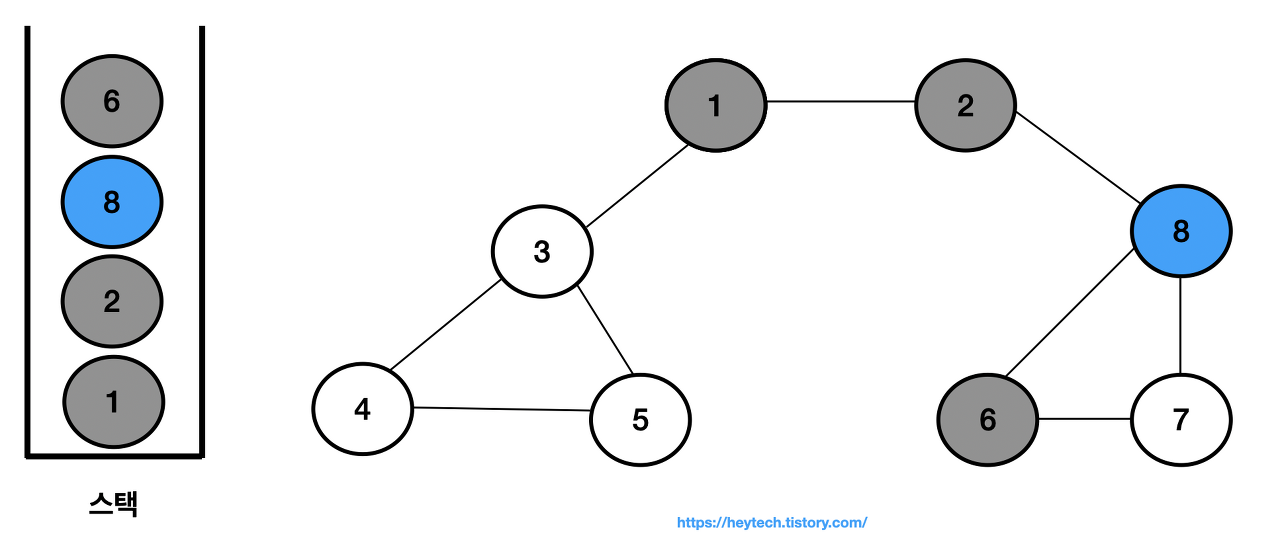
-
스택 내 최상단 노드인 노드 6에 인접하며 방문하지 않은 노드 7을 스택에 삽입하고 방문 처리한다.
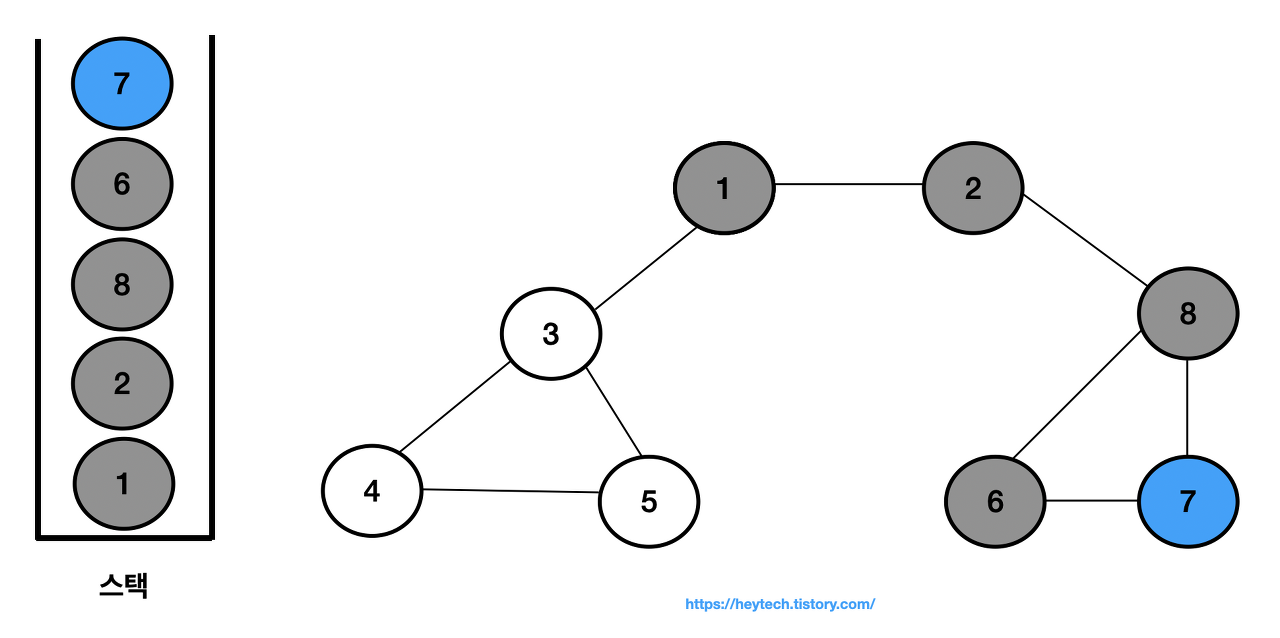
-
최상단 노드인 노드 7에 인접하며 방문하지 않은 노드가 없으므로 스택에서 노드 7을 꺼낸다.
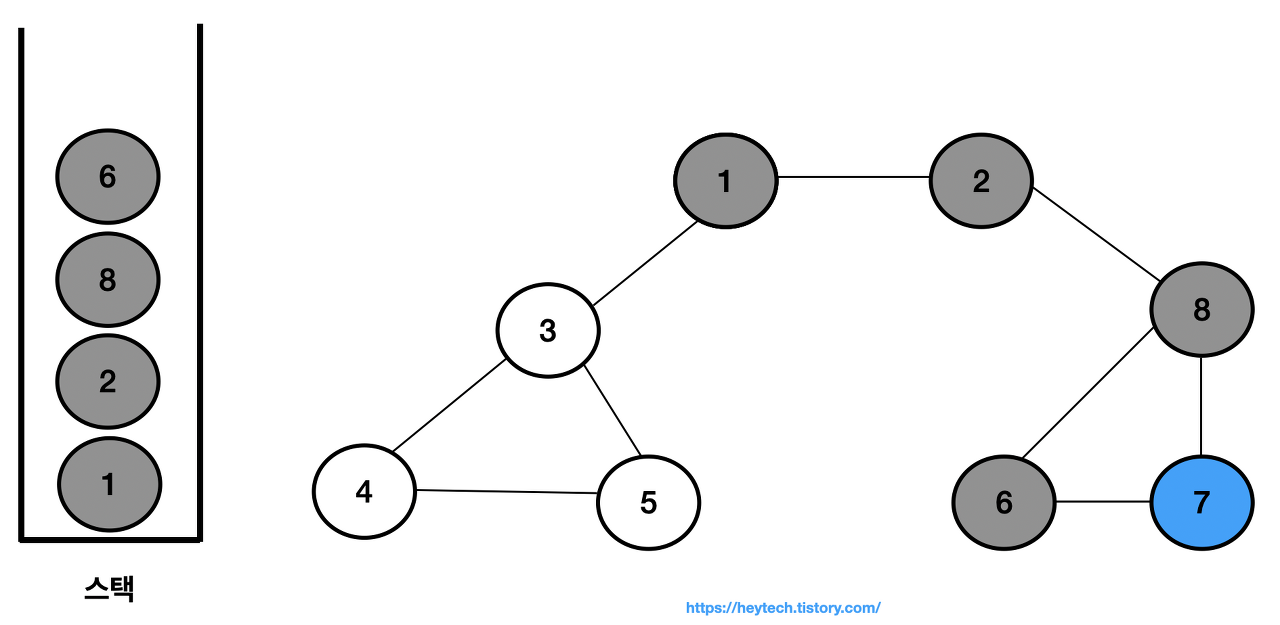
-
최상단 노드인 노드 6에 인접하며 방문하지 않은 노드가 없으므로 스택에서 노드 6을 꺼낸다.
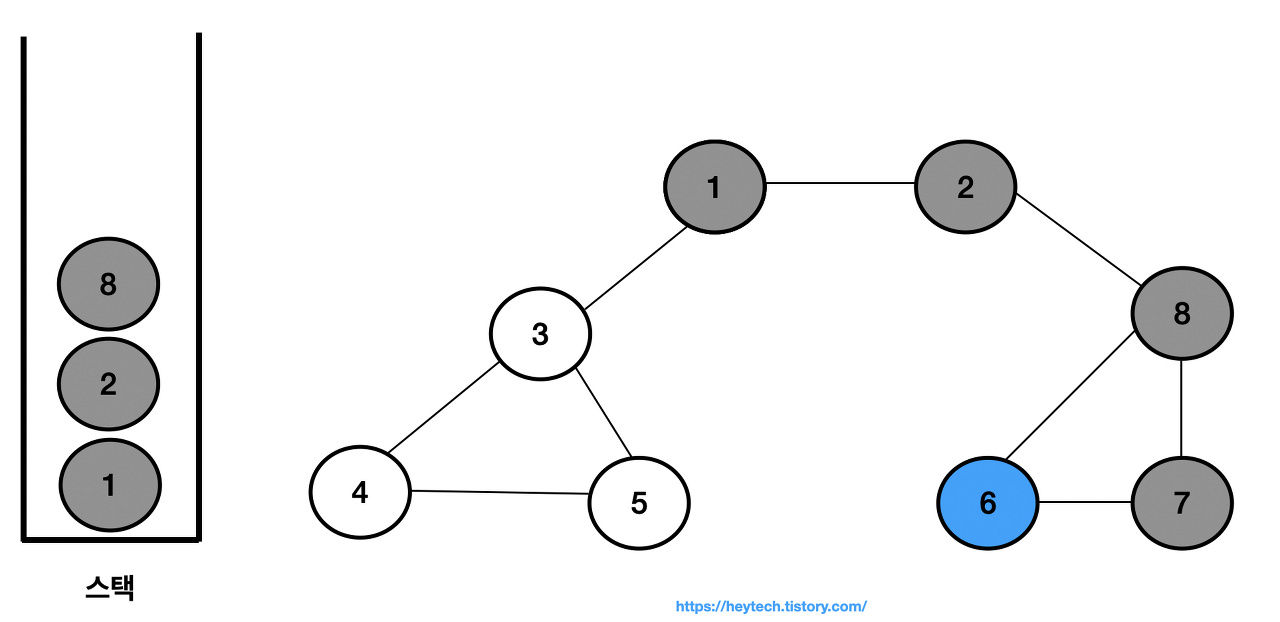
-
최상단 노드인 노드 8에도 인접하며 방문하지 않은 노드가 없으므로 스택에서 노드 8을 꺼낸다.
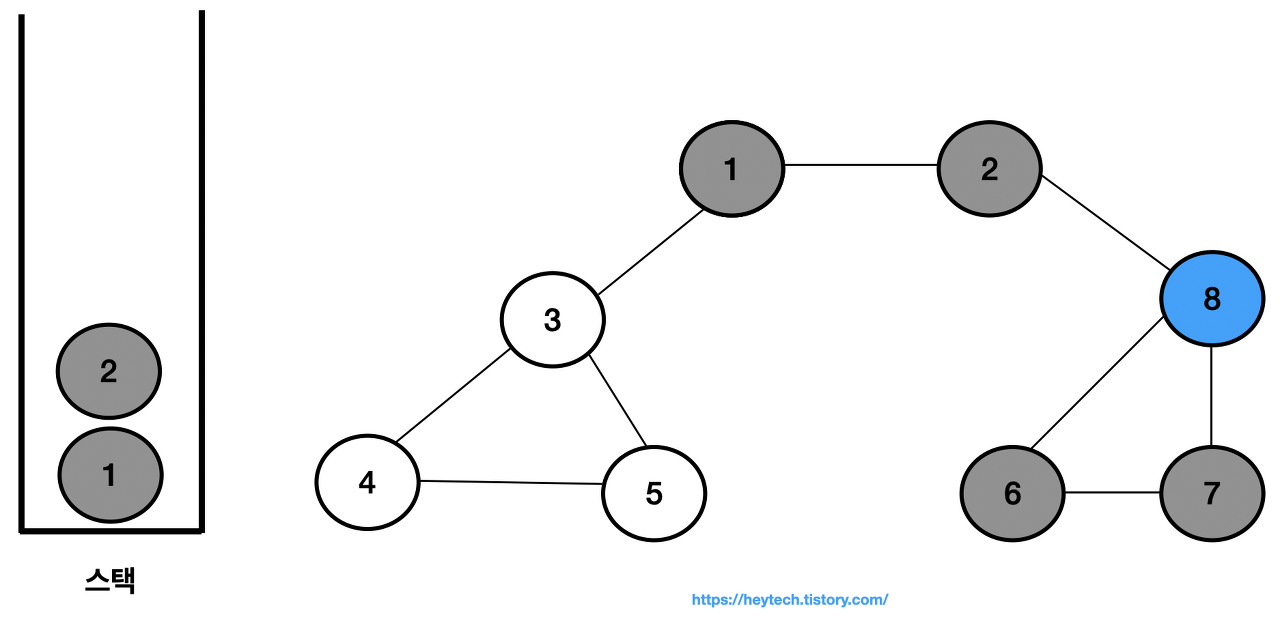
-
최상단 노드인 노드 2에 인접하며 방문하지 않은 노드가 없으므로 스택에서 노드 2를 꺼낸다.
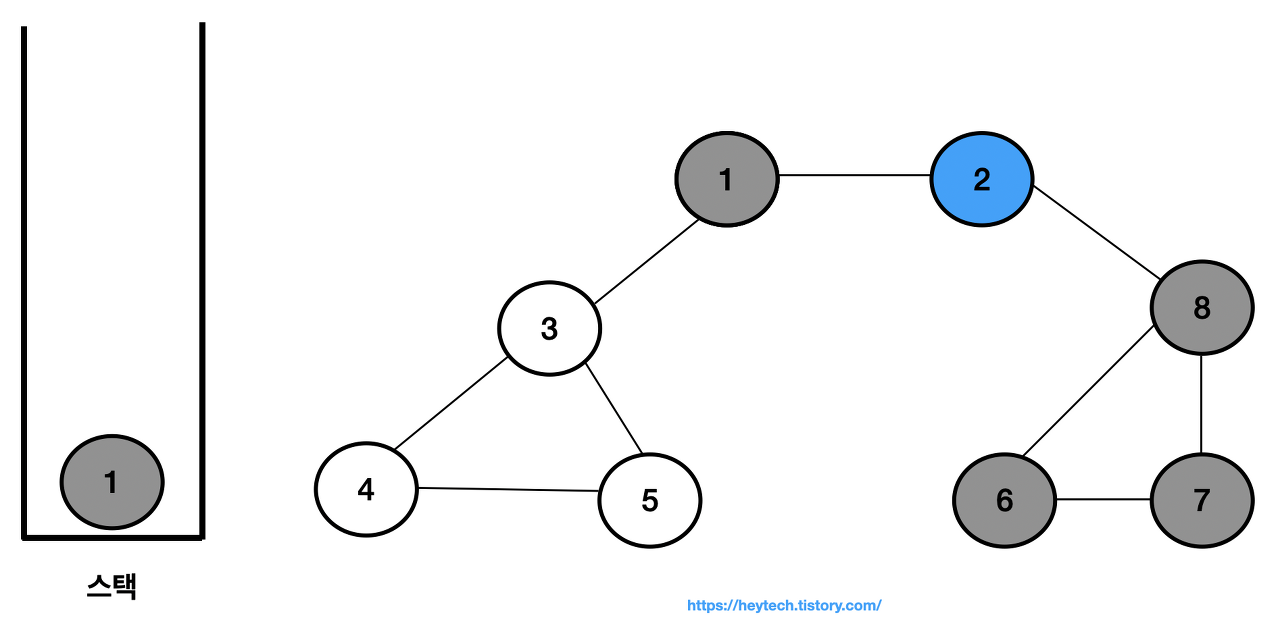
-
노드 1에 인접하면서 방문 이력이 없는 노드 3을 스택에 삽입하고 방문 처리한다.
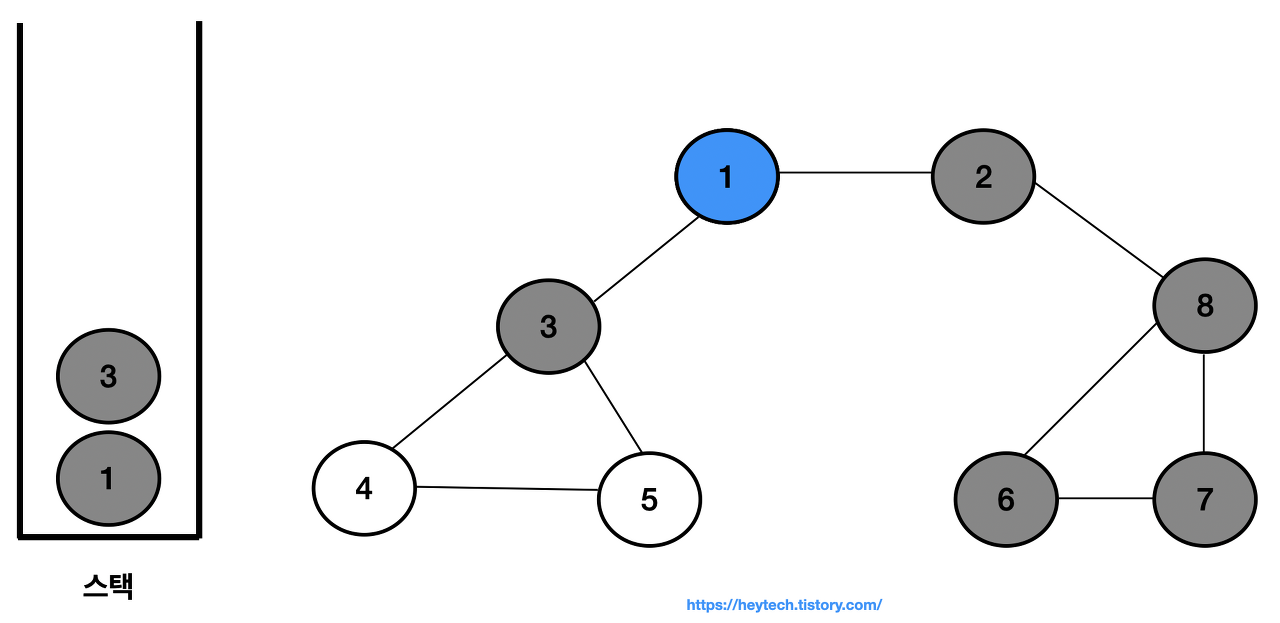
-
노드 3에 인접하면서 방문하지 않은 노드는 노드 4와 5가 있지만, 번호가 낮은 노드 4를 스택에 삽입하고 방문 처리한다.
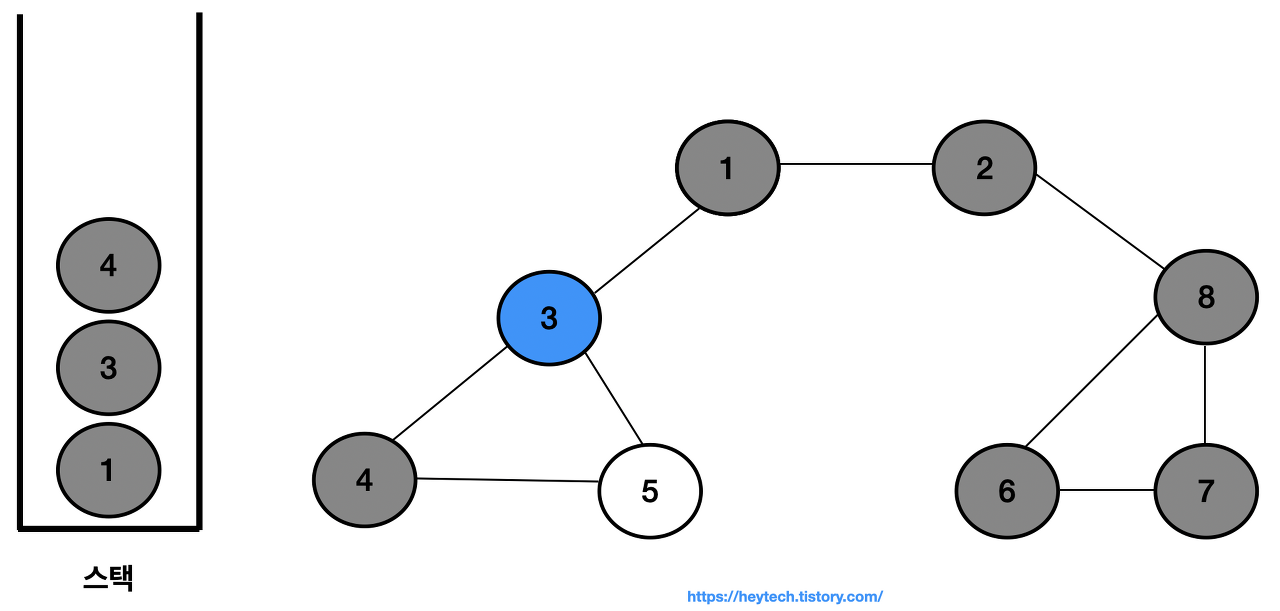
-
노드 4에 인접한 노드 5를 스택에 넣고 방문 처리한다.
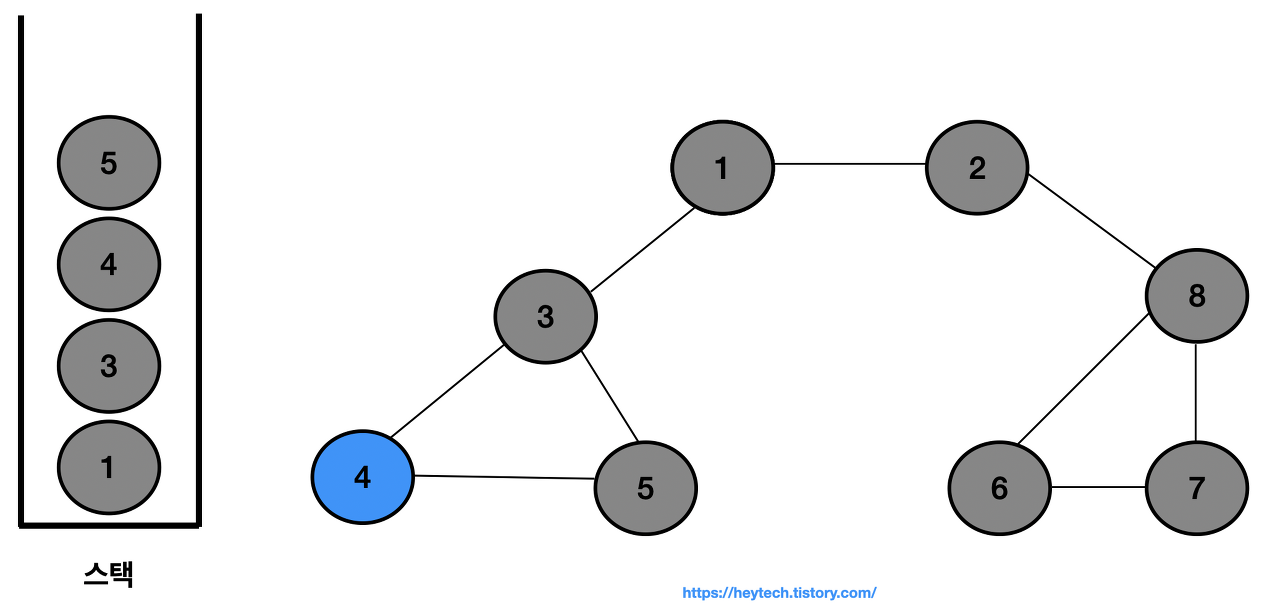
-
이제 방문하지 않은 노드가 없기 때문에 스택에서 모든 노드를 차례대로 꺼낸다.
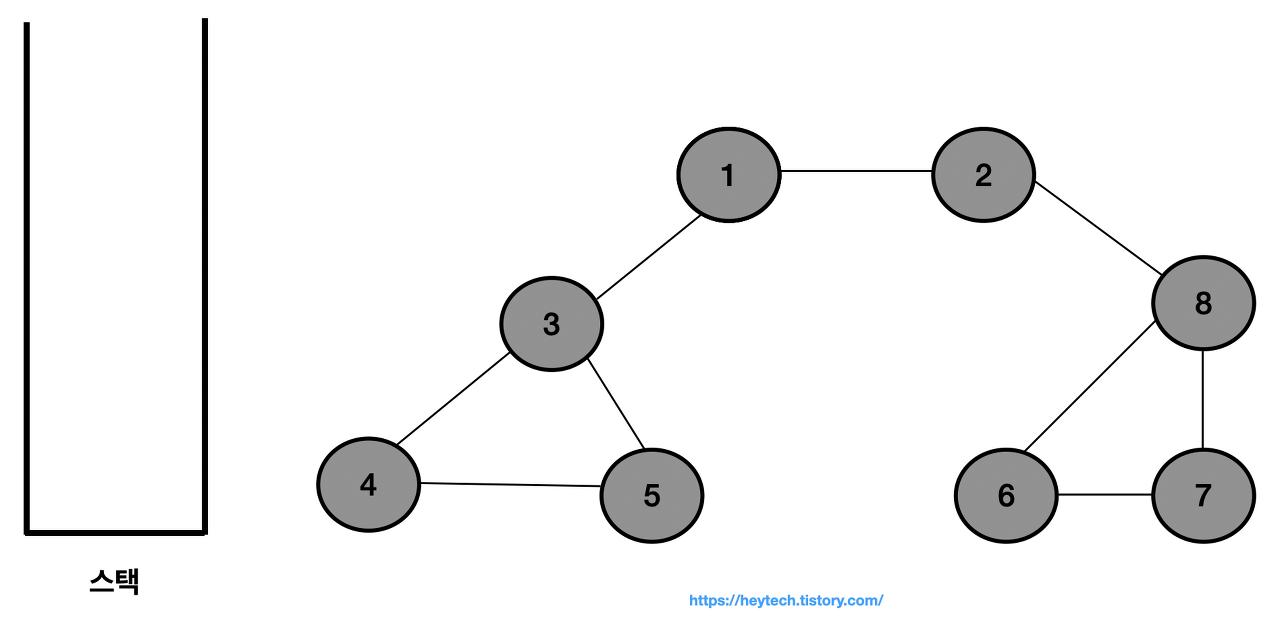
결과적으로 노드의 탐색 순서, 즉 스택에 삽입한 순서는 다음과 같다.
1 → 2 → 8 → 6 → 7 → 3 → 4 → 5
public class DFSSearch {
public ArrayList<String> dfsFunc(HashMap<String, ArrayList<String>> graph, String startNode){
ArrayList<String> visited = new ArrayList<>();
ArrayList<String> needVisit = new ArrayList<>();
needVisit.add(startNode);
while (needVisit.size()>0){
String node = needVisit.remove(needVisit.size()-1);
if (!visited.contains(node)){
visited.add(node);
needVisit.addAll(graph.get(node));
}
}
return visited;
}
public static void main(String[] args) {
HashMap<String, ArrayList<String>> graph = new HashMap<>();
graph.put("A", new ArrayList<>(Arrays.asList("B", "C")));
graph.put("B", new ArrayList<>(Arrays.asList("A", "D")));
graph.put("C", new ArrayList<>(Arrays.asList("A", "G", "H", "I")));
graph.put("D", new ArrayList<>(Arrays.asList("B", "E", "F")));
graph.put("E", new ArrayList<>(Arrays.asList("D")));
graph.put("F", new ArrayList<>(Arrays.asList("D")));
graph.put("G", new ArrayList<>(Arrays.asList("C")));
graph.put("H", new ArrayList<>(Arrays.asList("C")));
graph.put("I", new ArrayList<>(Arrays.asList("C", "J")));
graph.put("J", new ArrayList<>(Arrays.asList("I")));
DFSSearch dfsSearch = new DFSSearch();
System.out.println(dfsSearch.dfsFunc(graph,"A"));
}
}
복잡도
- 스택에 Node를 넣고 빼는 데 걸리는 시간
BFS를 할때 큐에 같은 Node가 들어갈 수 없었던 것처럼, DFS를 할때도 스택에 같은 Node가 두번 들어갈 수 없다.
스택을 사용해 맨 뒤에 삽입하고 맨 뒤에 있는 데이터를 꺼내오는 연산들은 O(1)로 할 수 있다.
최대 V개의 Node들이 스택에 들어갔다 나온다.
Node들이 스택에 들어갔다 나오는데 걸리는 총 시간은 O(V)라고 할 수 있다.
- 스택에서 뺀 Node들의 인접한 Node들을 도는데 걸리는 시간
스택에서 Node를 꺼낼 때마다, Node에 인접한 다른 Node들을 돈다. 이 부분은 다 합치면 얼마나 걸리까?
위에서 얘기했듯이 모든 Node는 스택에 한 번만 들어가서 한 번만 나올 수 있다.
Node가 한 번 나올 때마다 그 Node의 인접 리스트를 돈다.
그러니까 모든 Node들의 인접 리스트를 딱 한번만 돈다고 할 수 있다.
총 엣지 수가 E니까 이 단계도 총 E에 비례하는 만큼 실행된다고 할 수 있다.
스택에서 뺀 Node들의 인접한 Node들을 도는데 O(E) 가 걸린다.
일반적인 DFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 시간 복잡도: O(V + E)
