Jusung Kim

Android Developer

1 분 소요

algorithms17_image1.jpg

탐색은 여러 데이터 중에서 원하는 데이터를 찾아내는 것을 의미한다.

순차 탐색은 데이터가 담겨있는 배열을 앞에서부터 하나씩 비교해서 원하는 데이터를 찾는 방법이다.

algorithms17_image2.gif

구현

순차 탐색은 매우 간단하게 구현이 가능하다.

public class SequentialSearch {
    public Integer SearchNumberFun(ArrayList<Integer> integers, int searchNumber){
        for (int index = 0; index < integers.size(); index++){
            if (integers.get(index) == searchNumber){
                return integers.get(index);
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        ArrayList<Integer> testData = new ArrayList<>();
        for (int i = 0; i < 10; i++) {
            testData.add((int)(Math.random() * 100));
        }
        SequentialSearch sequentialSearch = new SequentialSearch();
        System.out.println(sequentialSearch.SearchNumberFun(testData, 63));
    }

}

복잡도

순차 탐색은 데이터 정렬 여부와 상관없이 가장 앞에 있는 원소부터 하나씩 확인해야 한다는 특징이 있다.

따라서, 데이터의 갯수가 N개 일 때 최대 N번의 비교 연산이 필요하므로 순차 탐색의 최악의 경우 시간 복잡도는 O(N)이다.

이진 탐색은 배열 내부의 데이터가 정렬되어 있어야한다.

탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법이다.

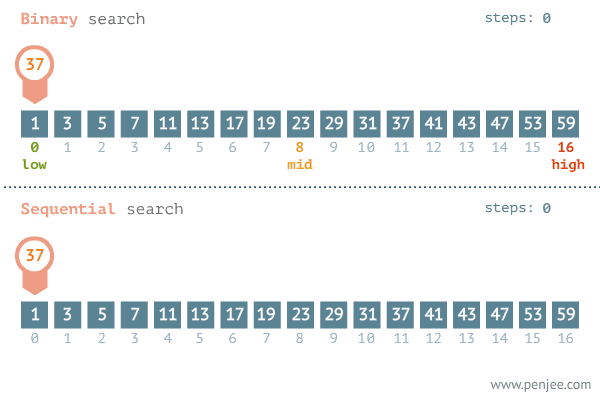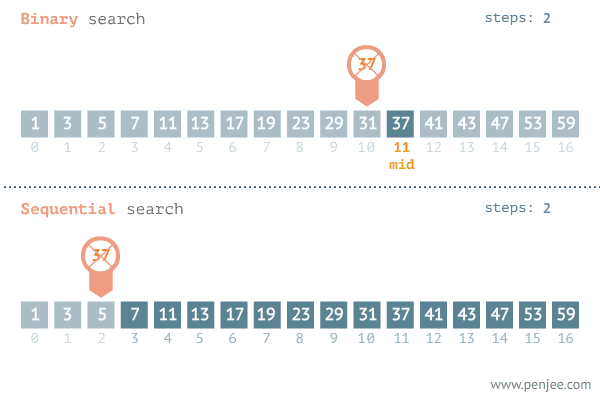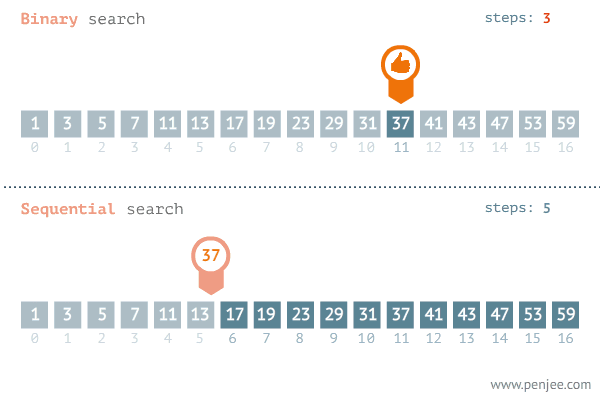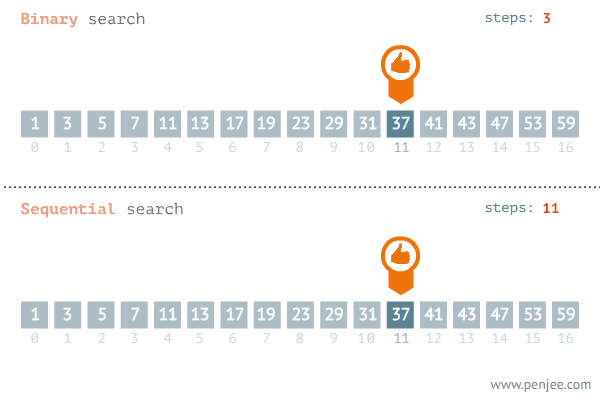
algorithms17_image3.gif

순차 탐색에 비해 상대적으로 빠르게 데이터를 찾는것을 알 수 있다.

구현

분할 정복 알고리즘을 생각하며 이진 탐색을 만들어본다.

  • 분할 정복 알고리즘
    • Divide: 문제를 하나 또는 둘 이상으로 나눈다.
    • Conquer: 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
  • 이진 탐색
    • Divide: 리스트를 두 개의 서브 리스트로 나눈다.
    • Conquer
      • (검색할 숫자 > 중간값) 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
      • (검색할 숫자 < 중간값) 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.
public class BinarySearch {
    public boolean searchFun(ArrayList<Integer> dataList, int findData){
        if (dataList.size() ==1 && dataList.get(0) == findData){return true;}
        if (dataList.size() == 1 && dataList.get(0) != findData){return false;}
        if (dataList.size() == 0){return false;}

        int medium = dataList.size() / 2;
        if (findData == dataList.get(medium)){
            return true;
        }else {
            if (findData < dataList.get(medium)){
                return this.searchFun(new ArrayList<>(dataList.subList(0,medium)),findData);
            }else {
                return this.searchFun(new ArrayList<>(dataList.subList(medium,dataList.size())),findData);
            }
        }
    }

    public static void main(String[] args) {
        ArrayList<Integer> testData = new ArrayList<>();
        for (int index = 0; index < 100; index++) {
            testData.add((int)(Math.random() * 100));
        }
        Collections.sort(testData);
        System.out.println(testData);
        BinarySearch bSearch = new BinarySearch();
        System.out.println(bSearch.searchFun(testData, 2));
    }
}

복잡도

이진 탐색은 한번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어든다는 점에서 O(logN)이다.

처음에 입력된 갯수를 N이라고하면, 첫 시행 후에는 반이 버려지기때문에 N/2이다. 두번째는 또 그반이 버려지기 때문에 1/2 x N/2, 3번째는 1/2 x 1/2 x N/2 이다.

그럼 K번 시행 후에는? (1/2)^K x N 개가 남게된다.

탐색을 반복하고 탐색이 끝나는 시점에는 데이터가 1개만 남을것이다. 즉 (1/2)^K x N = 1 이된다.

양 변에 2^K를 곱해주면 N = 2^K가 된다. 여기에 양변에 2를 밑으로하는 로그를 취하면

K = log2N이된다.

참고