Jusung Kim

Android Developer

2 분 소요

algorithms16_image1.jpg

퀵 정렬(quick sort)

분활 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑한다.

기준점(pivot)을 정해서, 기준점보다 작은 데이터는 왼쪽, 큰 데이터는 오른쪽으로 모은다.

각 왼쪽, 오른쪽은 재귀용법을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복한다.

병합할때는 왼쪽 + 기준점 + 오른쪽으로 합친다.

algorithms16_image2.gif

구현

먼저 간단하게 만들어보자

임의의 리스트에 맨 앞의 데이터를 기준으로 작은 데이터는 left변수에, 그렇지 않은 데이터는 right변수에 넣어 병합해 본다.

public class Split {
    public void splitFunc(ArrayList<Integer> dataList) {
        if (dataList.size() <= 1) {
            return ;
        }
        int pivot = dataList.get(0);
        
        ArrayList<Integer> leftArr = new ArrayList<Integer>();
        ArrayList<Integer> rightArr = new ArrayList<Integer>();        
        
        for (int index = 1; index < dataList.size(); index++) {
            if (dataList.get(index) > pivot) {
                rightArr.add(dataList.get(index));
            } else {
                leftArr.add(dataList.get(index));
            }
        }
        
        System.out.println(leftArr);
        System.out.println(pivot);
        System.out.println(rightArr);        
    }

	public static void main(String[] args) {
        Integer[] array = {4, 1, 2, 5, 7}; 
		ArrayList<Integer> list = new ArrayList<Integer>(Arrays.asList(array));

        Split quickSort = new Split();
        System.out.println(quickSort.splitFunc(list));
    }
}

잘나눠지는것을 확인할 수 있다. 이제 해당 기능을 재귀함수 형태로 만들어 리스트를 최소 크기로 분할하고 각각의 부분 배열들을 정렬하고 결합해본다.

  • 리스트 원소의 갯수가 한개이면 해당 리스트 리턴
  • 그렇지 않으면 맨 앞의 데이터를 기준점(pivot)으로 설정
  • 맨 앞의 데이터를 뺀 나머지 데이터를 기준점과 비교
    • 기준점 보다 작으면 left
    • 기준점 보다 크면 right
public class QuickSort {
    public ArrayList<Integer> sort(ArrayList<Integer> dataList){
        if (dataList.size()<=1){
            return dataList;
        }

        int pivot = dataList.get(0);
        ArrayList<Integer> leftList = new ArrayList<>();
        ArrayList<Integer> rightList = new ArrayList<>();

        for (int index = 1; index<dataList.size(); index++){
            if (dataList.get(index) < pivot){
                leftList.add(dataList.get(index));
            }else {
                rightList.add(dataList.get(index));
            }
        }

        ArrayList<Integer> mergeList = new ArrayList<>();
        mergeList.addAll(this.sort(leftList));
        mergeList.addAll(Arrays.asList(pivot));
        mergeList.addAll(this.sort(rightList));
        return mergeList;
    }

    public static void main(String[] args) {
        ArrayList<Integer> testData = new ArrayList<>();
        for (int index = 0; index < 100; index++) {
            testData.add((int)(Math.random() * 100));
        }
        QuickSort quickSort = new QuickSort();
        quickSort.sort(testData);
    }
}

복잡도

병합 정렬과 유사하다.

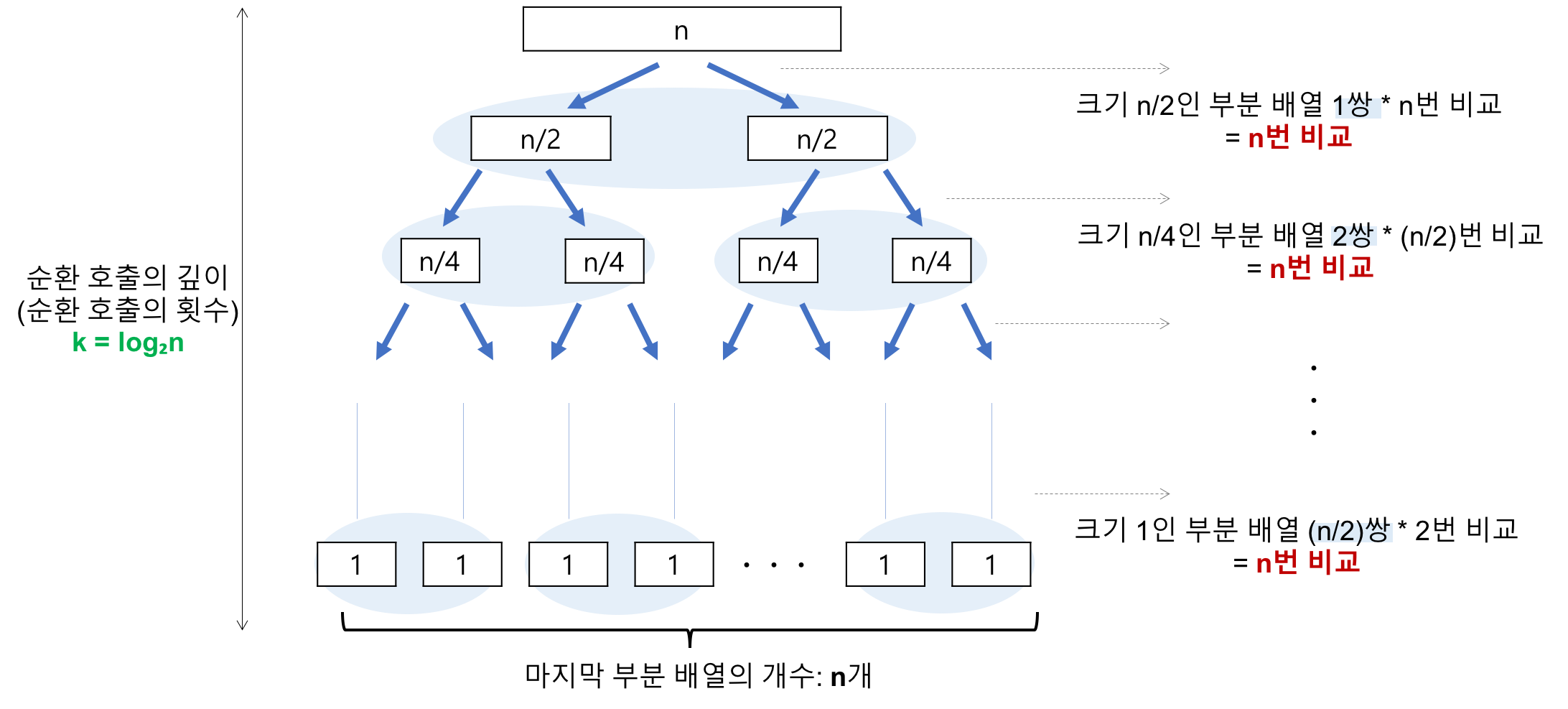
algorithms16_image3.png

  • 순환 호출의 깊이
    • 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
  • 각 순환 호출 단계의 비교 연산
    • 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
  • 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n

최악의 경우

최악의 경우는 정렬하고자 하는 배열이 오름차순이나 내림차순으로 이미 정렬되어있는 경우이다.

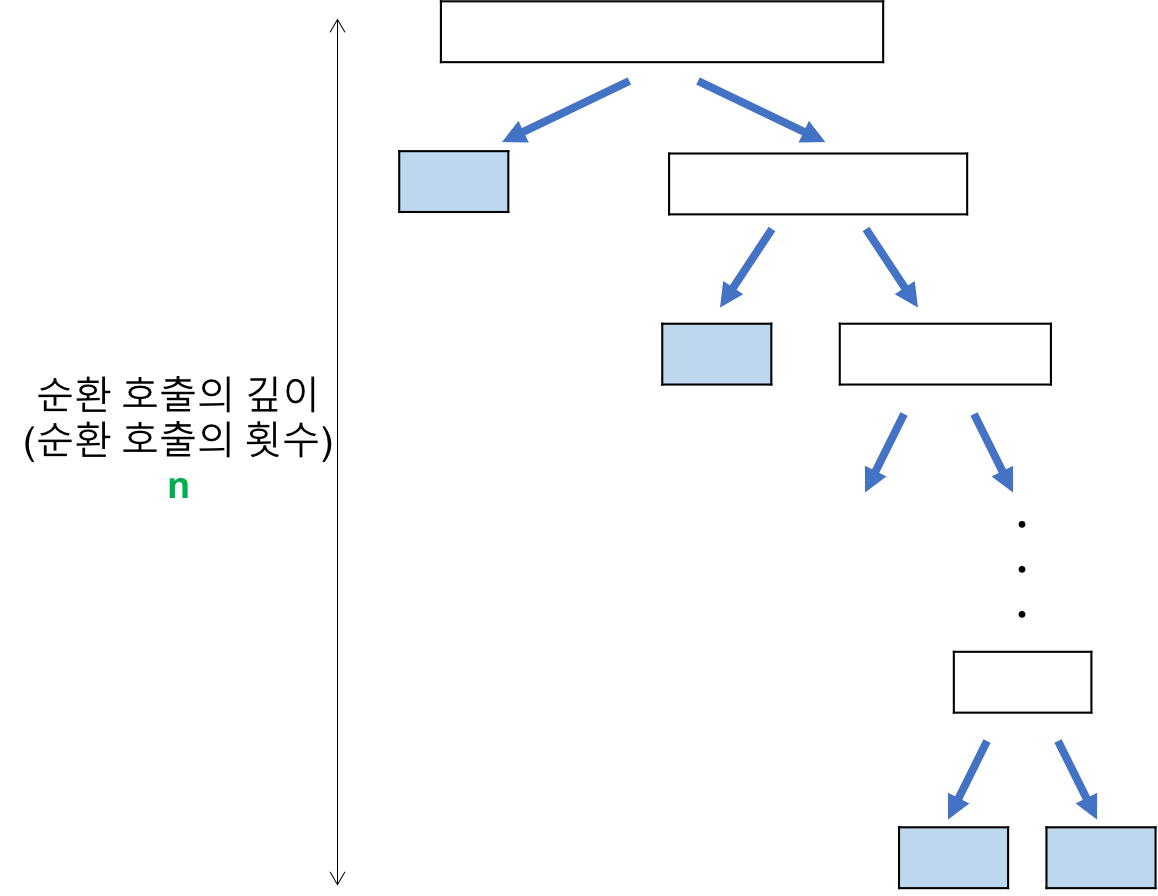
algorithms16_image4.png

  • 순환 호출 깊이
    • 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n임을 알 수 있다.
  • 각 순환 호출 단계의 비교 연산
    • 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
  • 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2

참조

https://gyoogle.dev/blog/algorithm/Quick Sort.html

참고