[Algorithm] 15장 고급 정렬 - 병합 정렬

병합 정렬(merge sort)
재귀용법을 활용한 정렬 알고리즘이다.
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

구현
재귀용법 틀를 먼저만들어본다.
- 배열의 갯수가 한개이면 해당 값 리턴
- 한개가 아니면 배열을 두개로 나눈다.
public ArrayList<Integer> mergeSplitFunc(ArrayList<Integer> dataList){
if (dataList.size()<=1){
return dataList;
}
int medium = dataList.size()/2;
ArrayList<Integer> leftArr;
ArrayList<Integer> rightArr;
leftArr = mergeSplitFunc(new ArrayList<>(dataList.subList(0,medium)));
rightArr = mergeSplitFunc(new ArrayList<>(dataList.subList(medium,dataList.size())));
return mergeFunc(leftArr,rightArr);
}
mergeFunc 함수는 아직 만들기 전이다. mergeFunc 함수가 leftArr과 rightArr를 합쳐서 정렬한 배열을 리턴한다.
합병과 재정렬하는 함수를 만든다.
public ArrayList<Integer> mergeFunc(ArrayList<Integer> leftArr, ArrayList<Integer> rightArr){
ArrayList<Integer> mergeList = new ArrayList<>();
int leftPoint = 0;
int rightPoint = 0;
while (leftArr.size()>leftPoint && rightArr.size()>rightPoint){
if (leftArr.get(leftPoint)>rightArr.get(rightPoint)){
mergeList.add(rightArr.get(rightPoint));
rightPoint++;
}else {
mergeList.add(leftArr.get(leftPoint));
leftPoint++;
}
}
while (leftArr.size()>leftPoint){
mergeList.add(leftArr.get(leftPoint));
leftPoint++;
}
while (rightArr.size()>rightPoint){
mergeList.add(rightArr.get(rightPoint));
rightPoint++;
}
return mergeList;
}
최종 코드는 다음과 같다.
public class MergeSort {
public ArrayList<Integer> mergeSplitFunc(ArrayList<Integer> dataList){
if (dataList.size()<=1){
return dataList;
}
int medium = dataList.size()/2;
ArrayList<Integer> leftArr;
ArrayList<Integer> rightArr;
leftArr = mergeSplitFunc(new ArrayList<>(dataList.subList(0,medium)));
rightArr = mergeSplitFunc(new ArrayList<>(dataList.subList(medium,dataList.size())));
return mergeFunc(leftArr,rightArr);
}
public ArrayList<Integer> mergeFunc(ArrayList<Integer> leftArr, ArrayList<Integer> rightArr){
ArrayList<Integer> mergeList = new ArrayList<>();
int leftPoint = 0;
int rightPoint = 0;
while (leftArr.size()>leftPoint && rightArr.size()>rightPoint){
if (leftArr.get(leftPoint)>rightArr.get(rightPoint)){
mergeList.add(rightArr.get(rightPoint));
rightPoint++;
}else {
mergeList.add(leftArr.get(leftPoint));
leftPoint++;
}
}
while (leftArr.size()>leftPoint){
mergeList.add(leftArr.get(leftPoint));
leftPoint++;
}
while (rightArr.size()>rightPoint){
mergeList.add(rightArr.get(rightPoint));
rightPoint++;
}
return mergeList;
}
public static void main(String[] args) {
ArrayList<Integer> testData = new ArrayList<>();
for (int index = 0; index < 100; index++) {
testData.add((int)(Math.random() * 100));
}
MergeSort mSort = new MergeSort();
System.out.println(mSort.mergeSplitFunc(testData));
}
}
복잡도
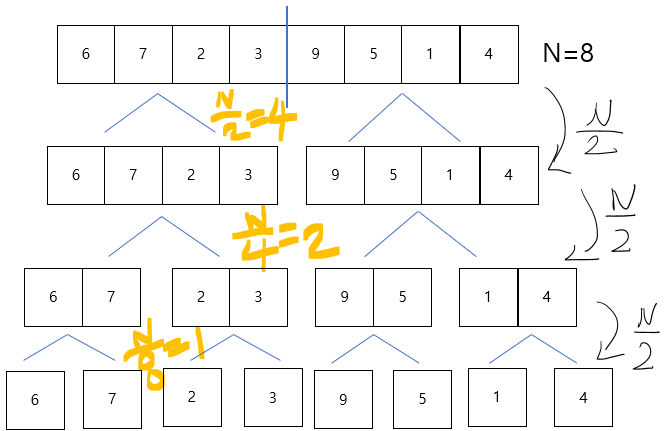
정렬되지 않은 8개의 숫자를 병합 알고리즘을 사용해 오름차순으로 정렬한다고 가정하자.
N=8인 배열을 한 개의 배열이 될 때까지 2로 나누면서(N/2) 분할한다.
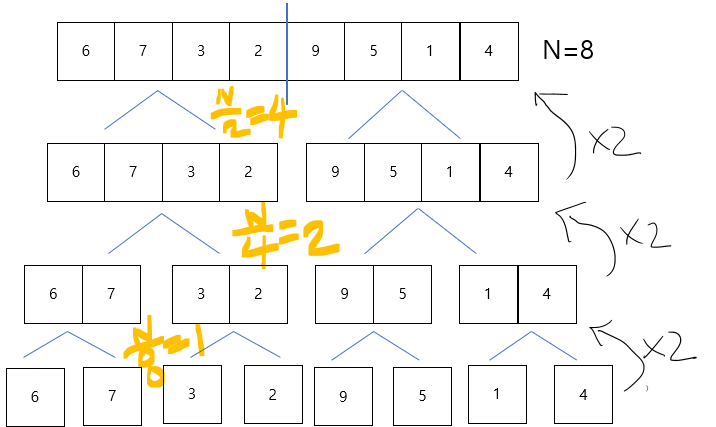
여기서 맨 아래에 한 개 씩 분활 된 것을 N=8로 다시 만들어 주려면 어떻게 해야할까?
위에서 2로 나눈 것과 반대로 2씩 곱해주어야 한다.
N=8이 되기 위해서 2를 몇번 곱해야할까?
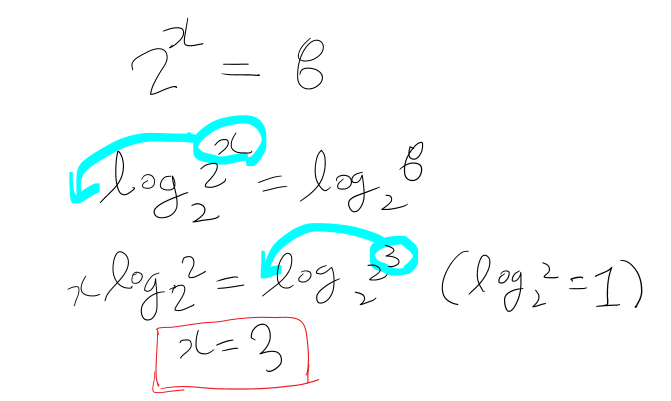
로그로 계산해보면 x = 3이 된다. 2를3번 곱해야 8이된다.

배열 원소 갯수가 N이라면 N이 되는데 2를 logN 만큼 곱해야한다.
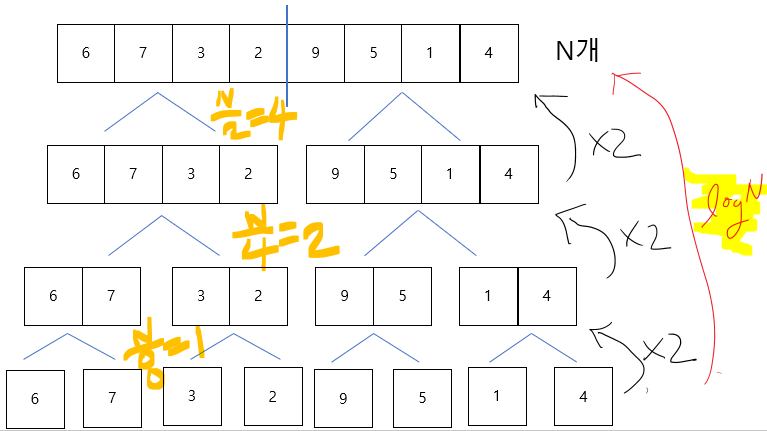
그렇다면 병합 알고리즘의 시간복잡도가 N*logN인 이유는 무엇인가.
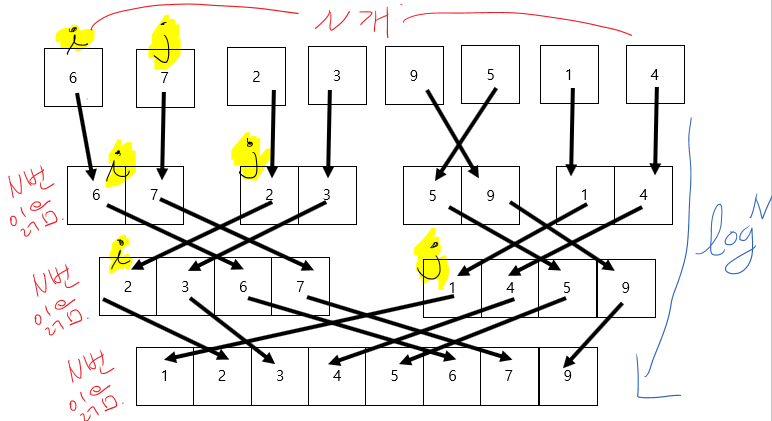
1개씩 분활 되었던 배열을 오름차순으로 정렬해가면서 병합하는 과정이다.
각 줄마다 모든 숫자 N개를 하나씩 읽어가면서 비교해서 병합한다.
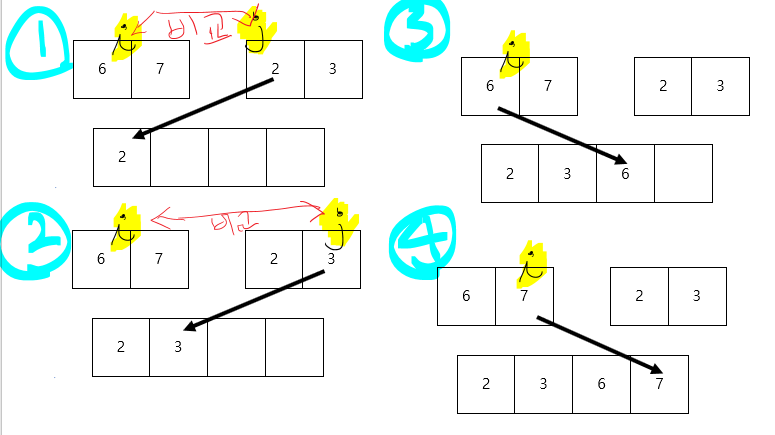
코드 구현 부분에서도 나와있듯이 순서대로 배열에 저장하기위해 모든 숫자를 비교한다.
그래서 최종적인 시간 복잡도는 O(N*logN)이 되는것이다.
