Jusung Kim

Android Developer

1 분 소요

algorithms13_image1.jpg

재귀 호출(recursive call)

자기 자신을 다시 호출하는 형태를 의미한다.

여러 알고리즘에서 자주 사용된다.

특징

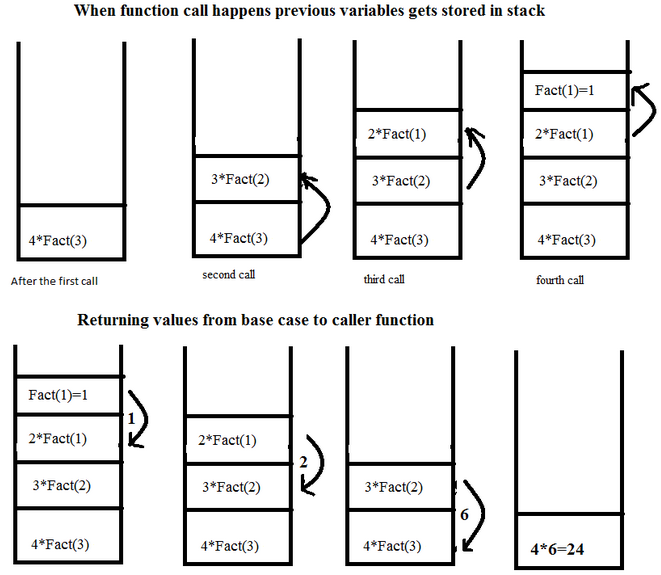
재귀 호출 함수는 내부적으로 스택처럼 관리된다. 스택처럼 호출한 함수를 쌓았다가 종료 조건을 만나면 위에서부터 하나씩 꺼내 처리한다.

algorithms13_image2.png

algorithms13_image3.webp

복잡도

factorial(n) 은 n - 1 번의 factorial() 함수를 호출해서, 곱셈을 한다.

일종의 n-1번 반복문을 호출한 것과 동일하다. factorial() 함수를 호출할 때마다, 지역변수 n 이 생성된다.

시간 복잡도, 공간 복잡도는 O(n-1) 이므로 결국, 둘 다 O(n)이다.

재귀 일반적 형태

종료 조건을 제대로 명시하지 않으면 함수가 무한히 호출되기 때문에 재귀 함수를 사용할 때는 재귀 함수의 종료 조건(제한)을 반드시 명시한다.

// 일반적인 형태1
function(입력) {
    if (입력 > 일정값) {        // 입력이 일정 값 이상이면
        return function(입력 - 1) // 입력보다 작은 값
    } else {
        return 특정값; // 재귀 호출 종료
    }
}

// 일반적인 형태2
function(입력) {
    if (입력 <= 일정값) {    // 입력이 일정 값보다 작으면
        return 특정값       // 재귀 호출 종료
    } 
    return function(입력 - 1);
}

반복문 비교

재귀 함수는 점화식과 종료조건만 구현하면 만들 수 있기 때문에 가시성이 높고, 구현하기 쉽다.

단 스택으로 쌓을 수 있는 정도가 정해져있다. 때문에 많은 호출이 필요할 때는 사용이 어렵다.

재귀함수와 반복문의 시간 복잡도는 동일하나 공간 복잡도로 볼때 메모리를 크게 차지한다.

예제

public class Factorial {

    public Integer unFactorial(Integer number){
        if (number>1){
            return number * this.unFactorial(number - 1);
        }else {
            return 1;
        }
    }

    public static void main(String[] args) {
        Factorial factorial = new Factorial();
        System.out.println(factorial.unFactorial(31));
    }
}

1번의 형태로 재귀 함수를 만들었다.

public class Factorial2 {

    public Integer unFactorial(Integer number){
        if (number<=1){
            return 1;
        }else {
            return number * this.unFactorial(number - 1);
        }
    }

    public static void main(String[] args) {
        Factorial2 factorial2 = new Factorial2();
        System.out.println(factorial2.unFactorial(31));
    }
}

2번의 형태로 재귀 함수를 만들었다.

참조

https://www.codecademy.com/learn/fscp-algorithms/modules/fecp-recursion/cheatsheet

참고