Jusung Kim

Android Developer

4 분 소요

algorithms9_image1.jpg

알고리즘 복잡도

  • 시간 복잡도 - 알고리즘 실행 속도
  • 공간 복잡도 - 알고리즘이 사용하는 메모리 사이즈

알고리즘 복잡도 계산이 왜 필요할까?

하나의 문제를 푸는 알고리즘은 다양할 수 있다.

예를들어 정수의 절대값을 구한다고하자. 두가지 정도의 방법을 생각할 수 있다.

  • 정수값을 제곱한 값에 다시 루트를 씌운다.
  • 정수가 음수인지 확인한뒤, 음수을 경우만 -1을 곱한다.

이렇게 다양한 알고리즘중 어느 알고리즘이 더 효율적인지 찾기위해 복잡도를 정의하고 계산한다.

가장 중요한 시간 복잡도를 의해하고 계산할 수 있어야한다.

시간 복잡도의 요소

알고리즘를 이루는 여러 요소들이 있다.(변수, 조건, 반복) 그중에서 가장 큰 영향을 미치는건 반복문이다.

예를들어 차를타고 서울에서 부산을 간다고 생각을 해보자. 출발해서 도착할때까지의 행동중 가장 총 시간에 영향을 끼지는 요소는 어떤것일까

  1. 자동차 문열기
  2. 자동차 문닫기
  3. 자동차 시트 조정
  4. 자동차 시동걸기
  5. 자동차로 서울에서 부산가기
  6. 자동차 시동끄기
  7. 자동차 문열기
  8. 자동차 문닫기

다른 요소들을 다합쳐서 몇분도 안되겠지만 서울에서 부산가는 요소는 몇시간이나 걸릴것이다. 총 걸리는 시간에 중요한 비중을 가진것이다.

마찬가지로 반복문이 시간 복잡도에 가장 영향을 미친다.

입력의 크기가 커지면 반복문이 알고리즘 수행 시간을 지배한다.

알고리즘 성능 표기법

  • Big O (빅-오) 표기법: O(N)
    • 알고리즘 최악의 실행 시간을 표기
    • 가장 많이/일반적으로 사용 - 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문
  • Ω (오메가) 표기법: Ω(N)
    • 오메가 표기법은 알고리즘 최상의 실행 시간을 표기
  • Θ (세타) 표기법: Θ(N)
    • 오메가 표기법은 알고리즘 평균 실행 시간을 표기

Big O 표기법

  • O(입력)
    • 입력 n 에 따라 결정되는 시간 복잡도 함수
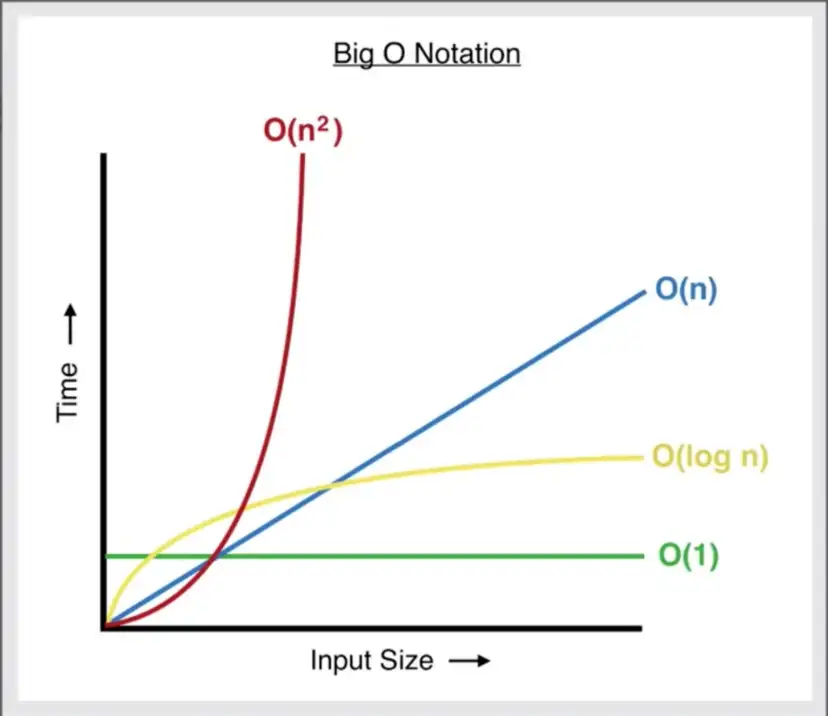
    • O(1), O(log n), O(n), O(nlog n), O(n^2), O(2^n), O(n!)등으로 표기한다.
    • 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있다.
    • O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!)
  • 입력 n에따라 몇번 실행되는지를 계산하면 된다.
    • 표현식에 가장 큰 영향을 미치는 n 의 단위로 표기한다.

    • n이 1이든 100이든, 1000이든, 10000이든 실행을 무조건 상수회 실행한다: O(1)

        //O(10)
  if (n > 10) { //10번 반복
  	System.out.println(n);
  }

    • n에 따라, n번, n + 10 번, 또는 3n + 10 번등 실행한다: O(n)

        //3*n = 3n -> O(n) 상수3은 영향을 끼치지 못한다.
  for (int num = 0; num < 3; num++) { //3번 반복
  	for (int index = 0; index < n; index++) { // n번 반복
  		System.out.println(index)
  	}
  }

    • n에 따라, n^2번, n^2 + 1000 번, 100n^2 - 100, 또는 300n^2 + 1번등 실행한다: O(n^2)

        //3*n*n = 3n^2 -> O(n^2) 상수3은 영향을 끼치지 못한다.
  for (int i = 0; i < 3; i++) { //3번 반복
  	for (int num = 0; num < n; num++) { //n번 반복
  		for (int index = 0; index < n; index++) {//n번 반복
  			System.out.println(index)
  		}
  	}
  }

algorithms9_image2.webp

시간 복잡도 구하기

1부터 n까지의 합을 구하는 알고리즘

알고리즘 1

  • 합을 기록할 변수를 만들고 0을 저장
  • n을 1부터 1씩 증가하면서 반복
  • 반복문 안에서 합을 기록할 변수에 1씩 증가된 값을 더함
  • 반복이 끝나면 합을 출력
public class Main {
	public int sum(int n) {
		int total = 0;
		for (int i = 1; i <= n; i++) {
			total += i;
		}
		return total;
	}
}

입력 n에 따라 덧셈을 n 번 해야 함 (반복문)

시간 복잡도: n, 빅 오 표기법으로는 O(n)

알고리즘2

  • $n(n+1)/2$
public class Main {
	public int sum(int n) {
		return n * (n + 1) / 2;
	}
}

입력 n이 어떻든 간에, 곱셈/덧셈/나눗셈 하면 된다. (반복문이 없다.)

시간 복잡도: 1, 빅 오 표기법으로는 O(1)

평가

  • 알고리즘1 vs 알고리즘2
    • O(n) vs O(1)

이와 같이, 동일한 문제를 푸는 알고리즘은 다양할 수 있다.

어느 알고리즘이 보다 좋은지를 객관적으로 비교하기 위해, 빅 오 표기법등의 시간복잡도 계산법을 사용한다.

공간 복잡도(Space Complexity)

좋은 알고리즘은 실행 시간이 짧고, 저장 공간도 적게 쓰는 알고리즘이다. 하지만 둘다 만족시키기는 어렵다.

  • 시간과 공간은 반비례적 경향이 있다.
  • 최근 대용량 시스템이 보편화되면서, 공간 복잡도보다는 시간 복잡도가 우선시된다.

그래도 공간 복잡도의 대략적인 계산은 필요하다.

  • 알고리즘 문제는 예전에 공간 복잡도도 고려되어야할 때 만들어진 경우가 많다.
  • 알고리즘 문제에 시간 복잡도뿐만 아니라, 공간 복잡도 제약 사항이 있는 경우가 있다.

공간 복잡도란

프로그램을 실행 및 완료하는데 필요한 저장공간의 양을 뜻한다.

  • 총 필요 저장 공간
    • 고정 공간 (알고리즘과 무관한 공간): 코드 저장 공간, 단순 변수 및 상수
    • 가변 공간 (알고리즘 실행과 관련있는 공간): 실행 중 동적으로 필요한 공간
    • S(P) = c + Sp(n)
      • c : 고정 공간
      • Sp(n) : 가변 공간

빅 오 표기법을 생각해볼 때, 고정 공간은 상수이므로 공간 복잡도는 가변 공간에 좌우 된다.

공간 복잡도 구하기

공간 복잡도 계산은 알고리즘에서 실제 사용되는 저장 공간을 계산하면 된다.(이를 빅 오 표기법으로 표현할 수 있으면된다.)

n! 팩토리얼을 구해본다. (n! = 1 x 2 x … x n)

알고리즘 1

public class Factorial {
    public int factorialFunc(int n) {
        int fac = 1;
        for (int index = 2; index < n + 1; index++) {
            fac = fac * index;
        }
        return fac;
    }
}

n의 값에 상관없이 변수 n, 변수 fac, 변수 index 만 필요하다.

공간 복잡도는 O(1)이다.

알고리즘 2

public class Factorial {
    public int factorialFunc(int n) {
        if (n > 1) {
            return n * factorialFunc(n - 1);
        } else {
            return 1;
        }
    }
}

재귀함수를 사용하였으므로, n에 따라, 변수 n이 n개가 만들어지게 된다.

factorial 함수를 재귀 함수로 1까지 호출하였을 경우, n부터 1까지 스택에 쌓이게 되고

공간 복잡도는 O(n)이다.

참고