[Algorithm] 7장 자료구조 - 트리(Tree)

트리(Tree)
Node로 이루어진 자료구조로 스택이나 큐와 같은 성형 구조가 아닌 비선형 구조이다.
트리는 계층적 관계를 표현하는 자료구조이다.
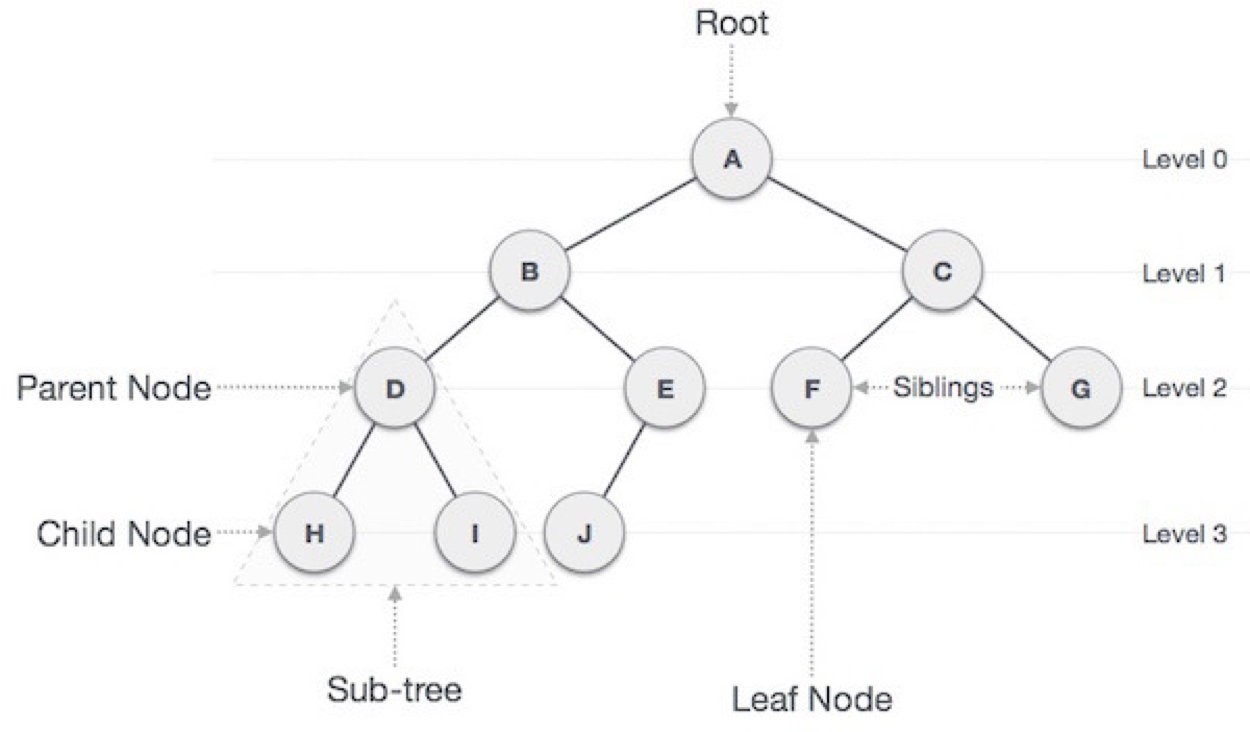
용어
- node - 트리에서 데이터를 저장하는 기본 요소
- root node - 트리 맨 위에 있는 노드
- leaf node - 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
- internal node - 단말 노드가 아닌 노드
- parent node - 어떤 노드의 상위 레벨에 연결된 노드
- child node - 어떤 노드의 다음 레벨에 연결된 노드
- sibling - 동일한 Parent Node를 가진 노드
- edge - 노드를 연결하는 선 (link, branch 라고도 부름)
- size - 자신을 포함한 모든 자손 노드의 개수
- depth - 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- level - 트리의 특정 깊이를 가지는 노드의 집합
이진 트리와 이진 탐색 트리(Binary Search Tree)
- 이진 트리 - 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리 (Binary Search Tree, BST) - 이진 트리에 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있다.

이진 탐색 트리의 용도
배열같은 구조에 비해 탐색 속도가 빠르기때문에 데이터 검색에 사용된다.
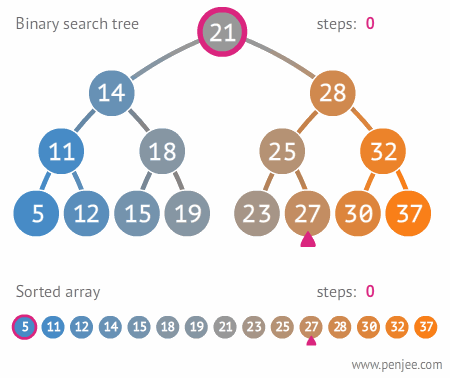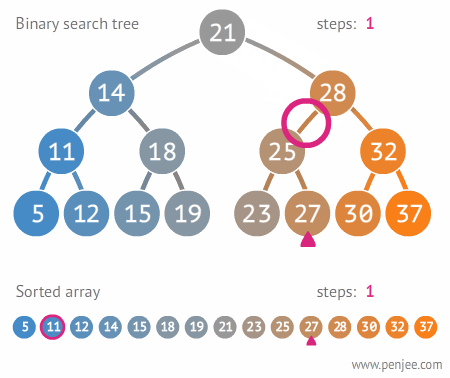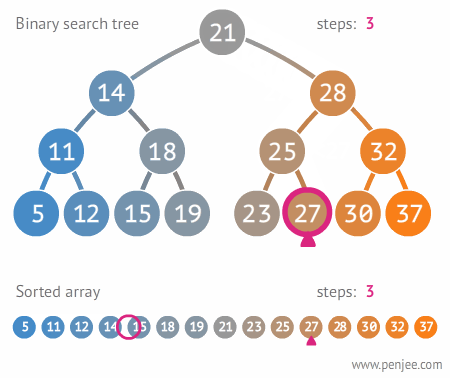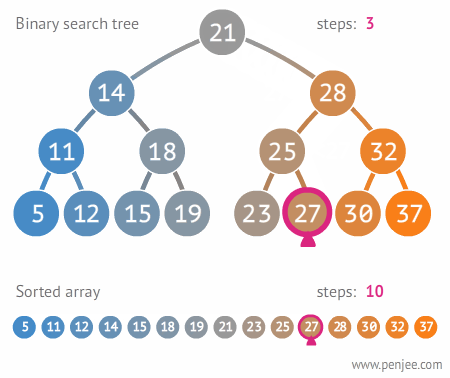
- depth(트리의 높이)를 h라고 표기한다면, O(h)
- n개의 노드를 가진다면, h = log2 n에 가까우므로 시간 복잡도는 O(logn)이다.
- 빅오 표기법에서 logn에서의 log의 밑은 10이 아니라 2이다.
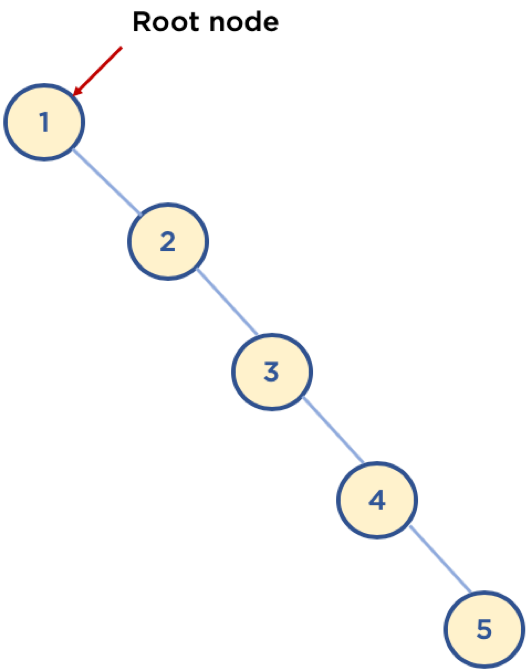
단점
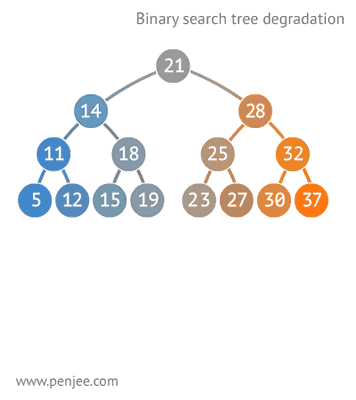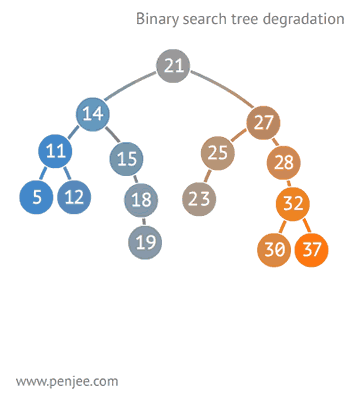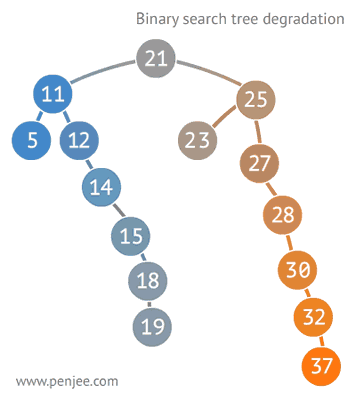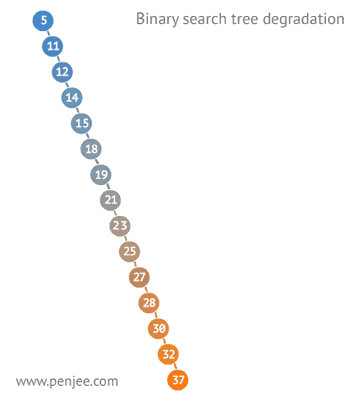
평균 시간 복잡도는 O(logn)이다. 이는 트리가 균형잡혀 있을때의 시간 복잡도이다.
다음과 같이 구성되어 있을 경우, 최악의 경우 링크드 리스트와 동일한 성능을 보여준다. O(n)
이진 탐색 트리 만들기
간단한 이진 탐색 트리를 만들어 보자.
노드 클래스 만들기
먼저 트리를 구성할 노드 클래스를 만든다. 이진 트리기때문에 좌, 우 노드 변수를 추가해준다.
public class MyTree {
Node root = null;
public class Node{
Node left;
Node right;
int value;
public Node(int value){
this.value = value;
this.left = null;
this.right = null;
}
}
}
노드 추가 메소드
public class MyTree {
Node root = null;
public class Node{
Node left;
Node right;
int value;
public Node(int value){
this.value = value;
this.left = null;
this.right = null;
}
}
public boolean addNode(int value){
//노드가 하나도 없을때
if (root == null){
root = new Node(value);
return true;
}else {
//노드가 이미 있을때
Node findNode = this.root;
while (true){
//기준 노드 값보다 작아 왼쪽 노드로 들어갈때
if (value < findNode.value){
if (findNode.left != null){
findNode = findNode.left;
}else {
findNode.left = new Node(value);
return true;
}
}else { //노드가 오른 쪽으로 들어갈때
if (findNode.right != null){
findNode = findNode.right;
}else {
findNode.right = new Node(value);
return true;
}
}
}
}
}
}
만약 루트 노드가 없으면 추가하는 데이터를 루트 노드로 만들어 준다.
루트 노드가 이미 있다면 그다음부터는 반복문으로 부모 노드보다 작으면 왼쪽으로 크면 오른쪽으로해서 진행한뒤 끝에 다다르면 노드를 추가해준다.
노드 탐색 메소드
public class MyTree {
Node root = null;
public class Node{
Node left;
Node right;
int value;
public Node(int value){
this.value = value;
this.left = null;
this.right = null;
}
}
public Node search(int value){
if (this.root != null) {
Node findNode = this.root;
while (findNode != null) {
if (findNode.value == value) {
return findNode;
} else if (value <= findNode.value) {
findNode = findNode.left;
} else {
findNode = findNode.right;
}
}
}
return null;
}
}
찾는 메소드도 추가 메소드와 비슷하다
노드의 값을 비교해서 작으면 왼쪽으로 크면 오른쪽으로 이동하고 동일한 값을 찾으면 해당 노드를 반환한다.
노드 삭제 메소드
지금까지는 기존 자료구조 처리와 비슷했으나 삭제는 어렵다. 하나하나 확인해 보겠다.
- leaf node 삭제
삭제할 노드의 부모 노드가 삭제할 노드를 가리키지 않도록 하면된다.
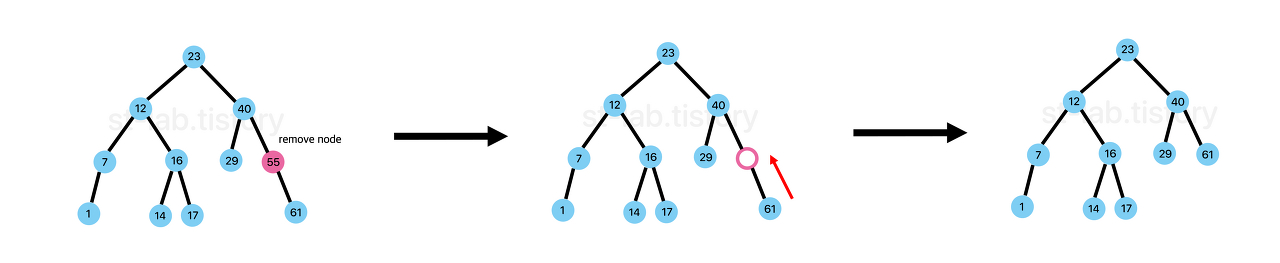
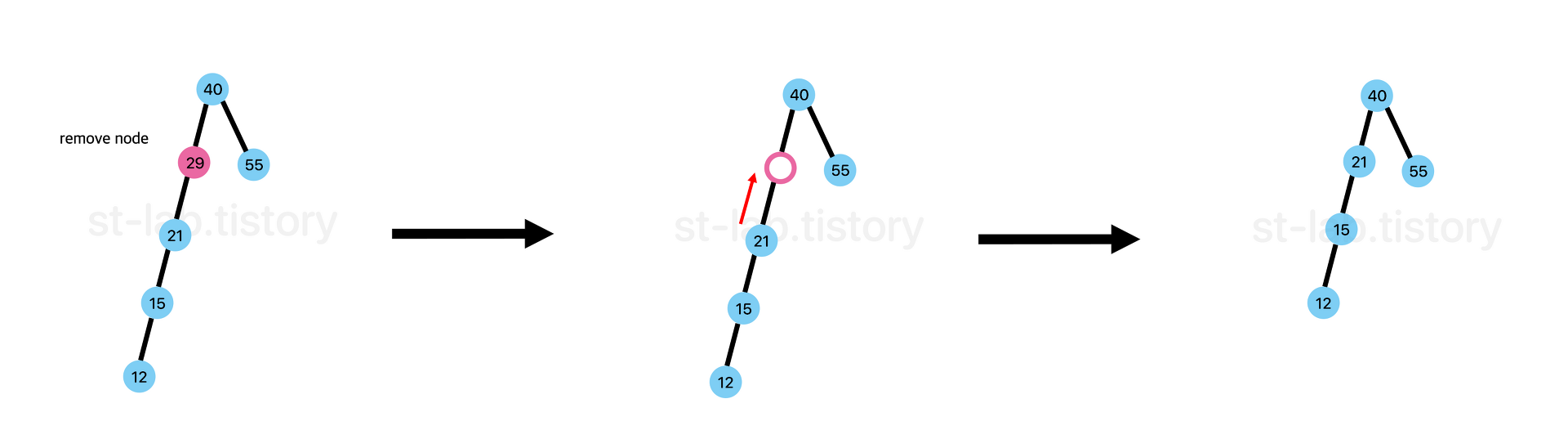
- child node가 하나인 node삭제
삭제할 노드의 부모 노드가 삭제할 노드의 자식노드를 가리키도록 한다.
- child node가 두개인 node삭제
- 삭제할 노드의 오른쪽 자식 중 가장 작은 값을 삭제할 노드의 부모 노드가 가리키도록 한다.
- 삭제할 노드의 왼쪽 자식 중 가장 작은 값을 삭제할 노드의 부모 노드가 가리키도록 한다.
자식 노드가 2개일때 왜 이런식으로 삭제를 해야할까?
자기 노드보다 작은 것은 왼쪽 자식노드로, 자기 노드보다 큰 노드는 오른쪽 자식노드로 갖는다.
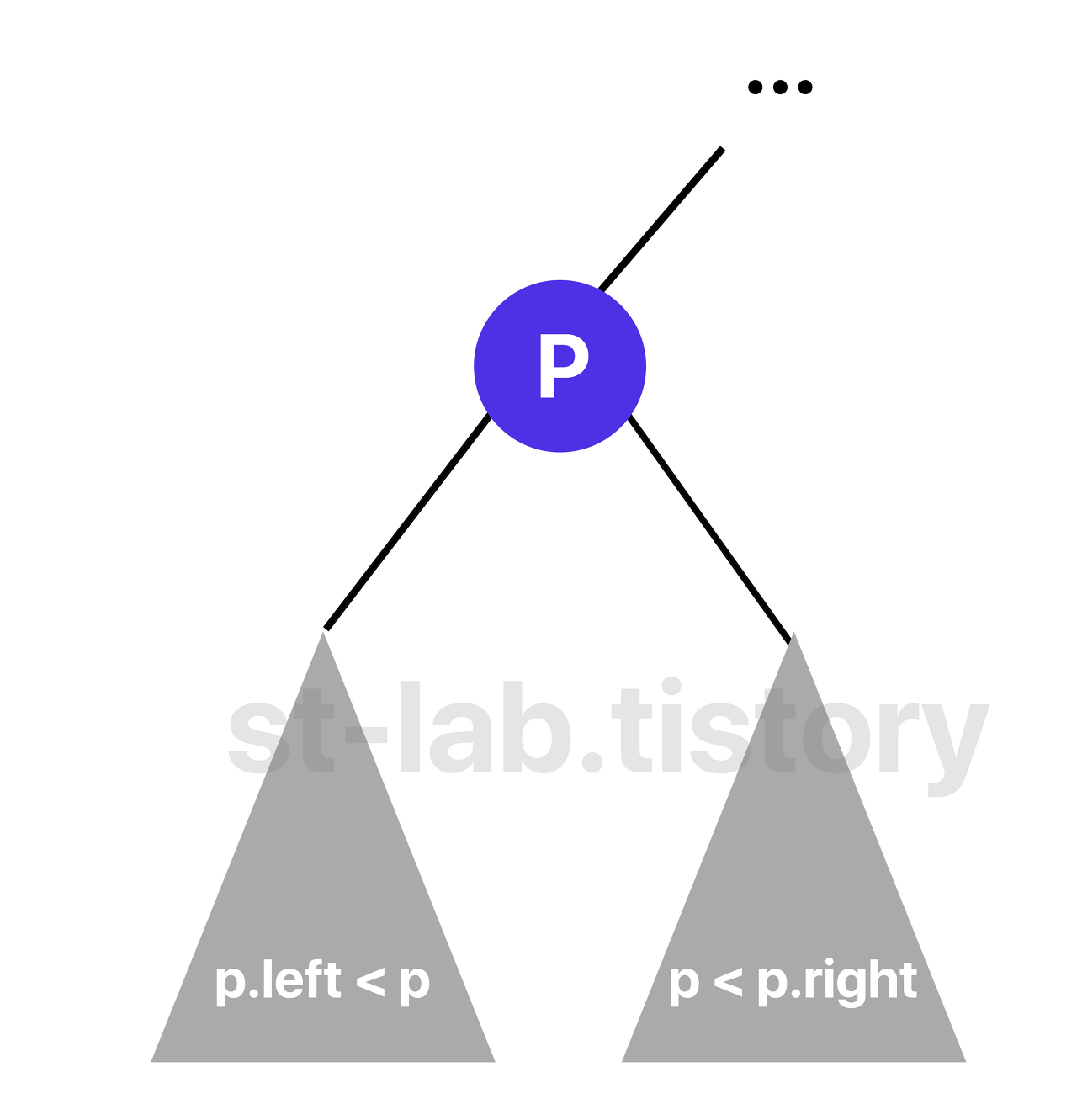
그렇다면 P 노드에서 값이 가장 가까운 두 노드는 무엇일까? 바로 P 왼쪽 자식노드에서 가장 오른쪽에 있는 노드, 그리고 P의 오른쪽 자식노드에서 가장 왼쪽에 있는 노드가 된다.
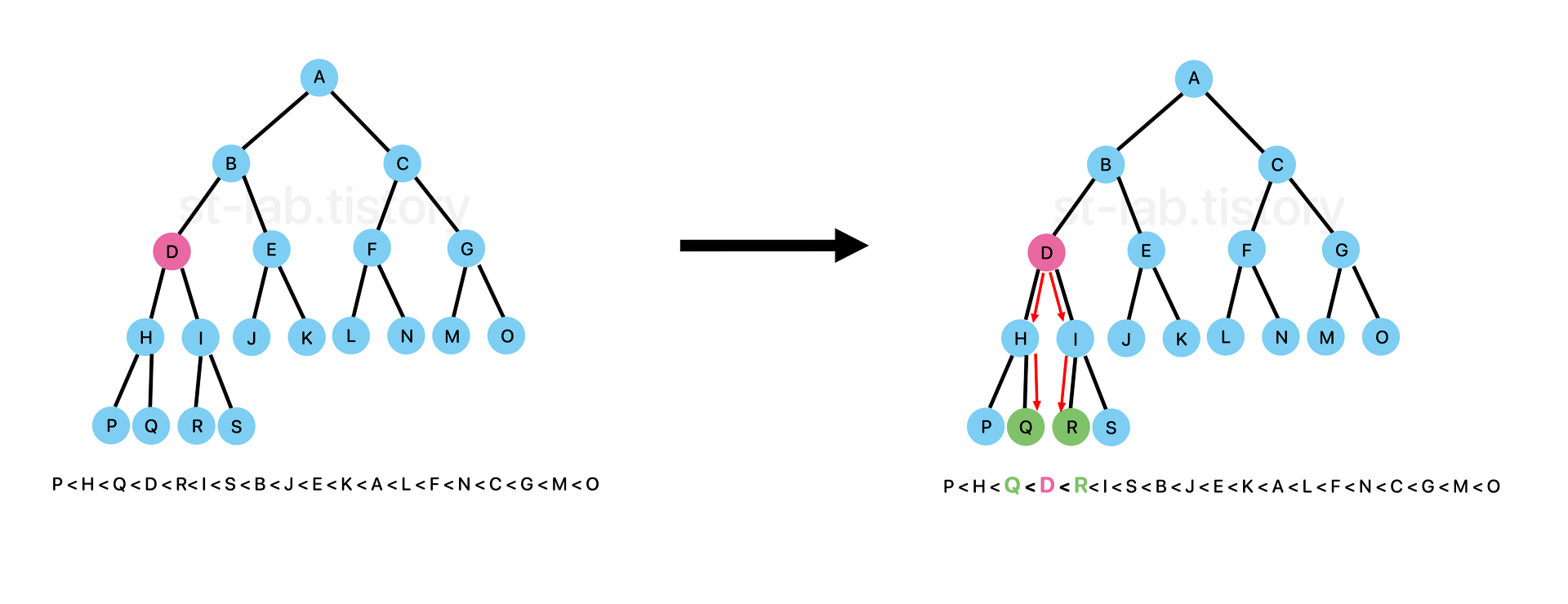
D노드를 기준으로 가장 가까운 값을 가지는 노드는 Q와 R노드이다. 코드는 첫번째 방법으로 삭제 메소드를 구현하겠다.
노드를 삭제하는 시나리오를 생각해보자.
삭제할 노드는 찾았다고 가정하고, 삭제할 노드에서 가장 가까운 노드를 찾아야한다. 오른쪽 자식 노드에서 가장 작은 노드를 탐색한다면 계속 왼쪽 노드를 찾아나가면 된다. 대체할 노드가 선정되었다면 해당 노드를 원래 참고하고 있던 부모 노드와의 링크도 끊어주어야 한다.
그리고 가장 작은 노드를 찾았을때 그 노드가 자식 노드를 가지고 있을 수 있다. 물론 가장 작기 때문에 왼쪽에는 없을 것이고 오른쪽 자식에 노드가 있을 수 있다.
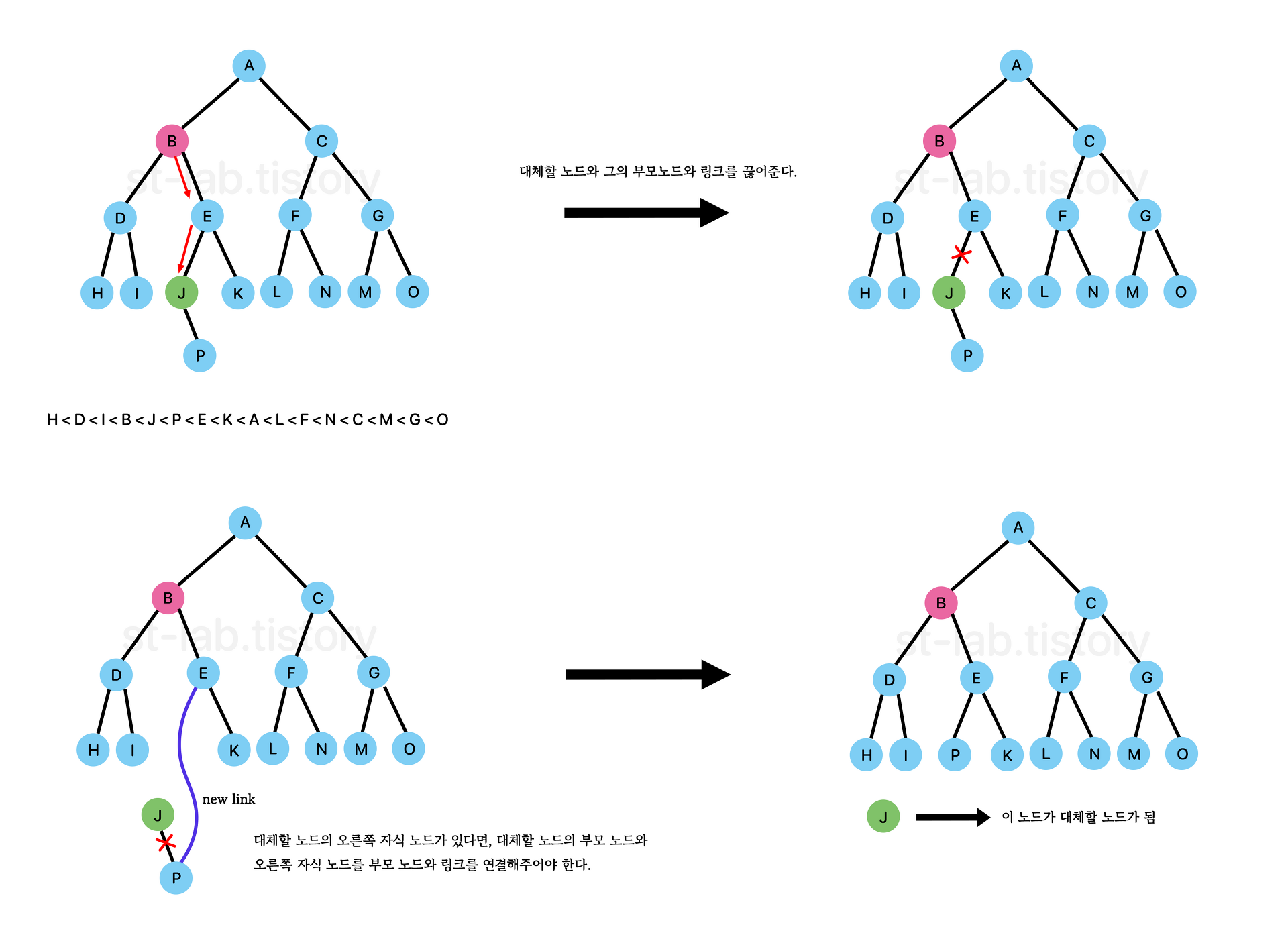
위 처럼 B노드의 오른쪽 자식 노드(E)를 기준으로 가장 작은 노드는 J노드다. 하지만 E와 J노드만 연결을 끊어주면 끝나는 것이 아니라, J노드의 오른쪽 자식노드가 있다면 이를 E노드와 연결을 해주어야한다.
정리 해서 코드상으로 구현할 상황은 다음과 같다.
- node가 하나만 있고 그 노드를 삭제해야 할 경우
-
삭제할 노드가 leaf 노드일경우
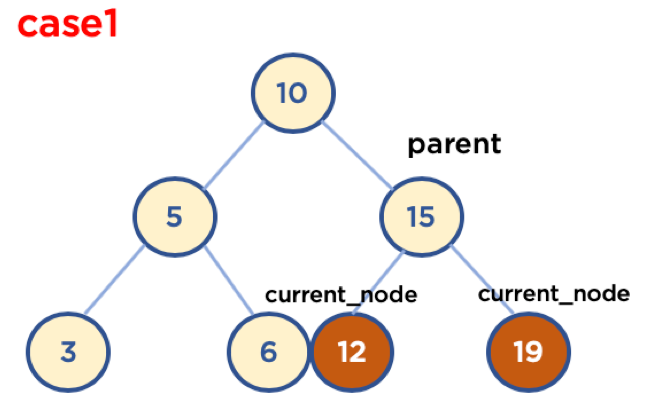
- 부모 노드의 왼쪽에 있을때
- 부모 노드의 오른쪽에 있을때
-
삭제할 노드가 자식 노드를 한개 가지고있을때
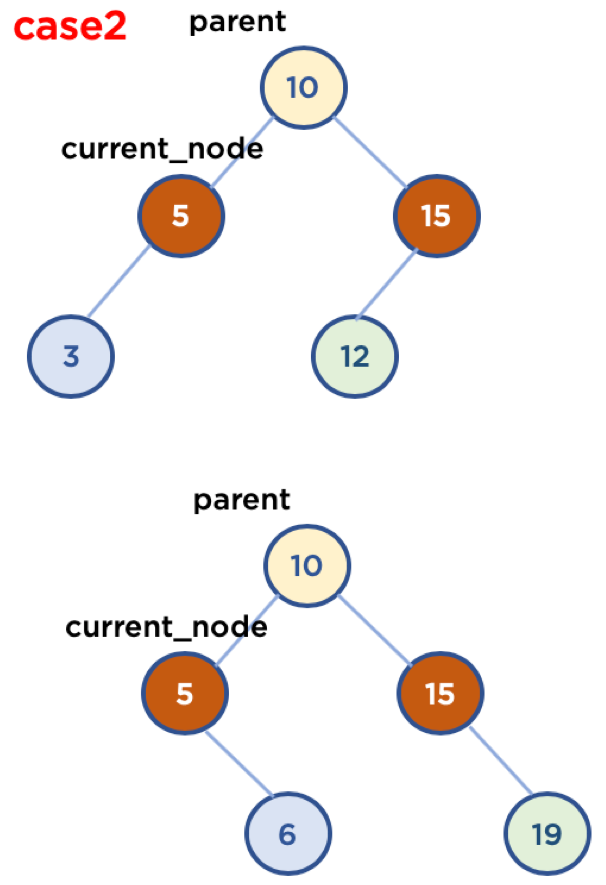
- 왼쪽에 자식노드
- 부모 노드의 왼쪽에 있을때
- 부모 노드의 오른쪽에 있을때
- 오른쪽에 자식노드
- 부모 노드의 왼쪽에 있을때
- 부모 노드의 오른쪽에 있을때
- 왼쪽에 자식노드
- 삭제할 노드가 자식 노드를 두 개 가지고 있을때
-
부모 노드의 왼쪽에 있을때
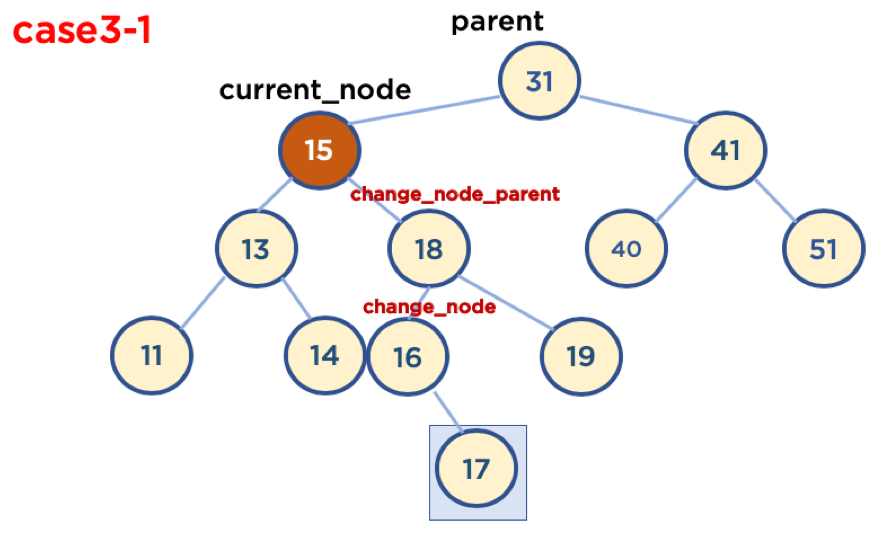
- 오른쪽에 자식 노드가 있을때
- 자식 노드가 없을때
-
부모 노드의 오른쪽에 있을때
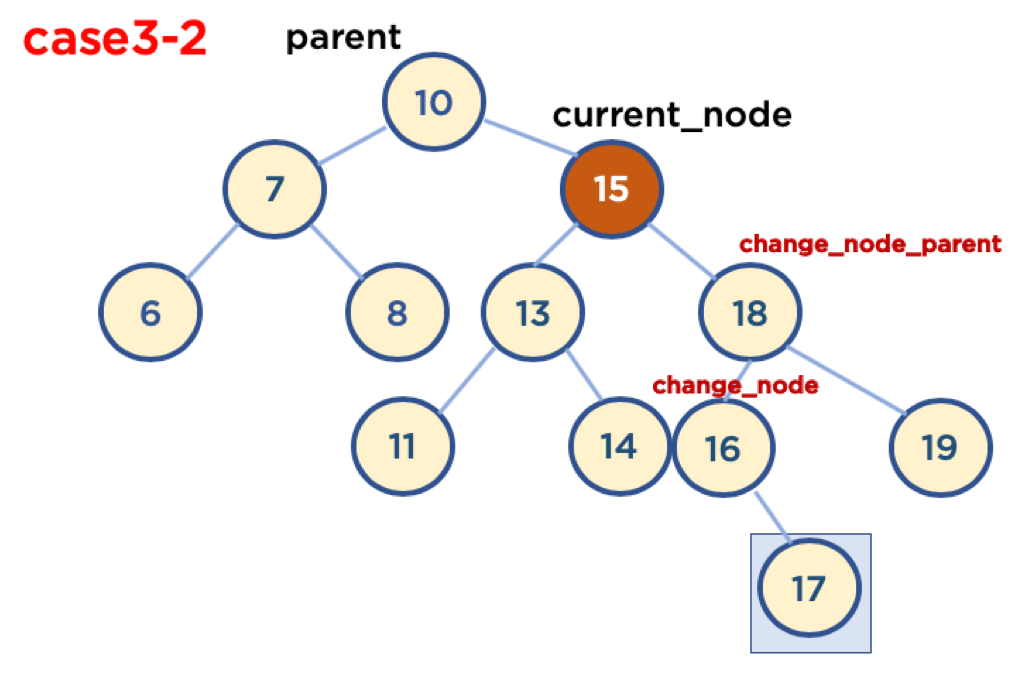
- 오른쪽에 자식 노드가 있을때
- 자식 노드가 없을때
-
이제 해당 내용을 코드로 구현해 보자.
public class MyTree {
Node root = null;
public class Node{
Node left;
Node right;
int value;
public Node(int value){
this.value = value;
this.left = null;
this.right = null;
}
}
public boolean delete(int value){
boolean searched = false;
Node currParentNode = this.root;
Node currNode = this.root;
/* Node 가 하나도 없을때 */
if (this.root == null){
return false;
}else {
/* Node 가 하나만 있고 그 노드를 삭제해야할 경우*/
if (this.root.value == value && this.root.left == null && this.root.right == null){
this.root = null;
return true;
}
/* 삭제할 노드를 찾는다. */
while (currNode != null){
if (currNode.value == value){
searched = true;
break;
}else if (value < currNode.value){
currParentNode = currNode;
currNode = currNode.left;
}else {
currParentNode = currNode;
currNode = currNode.right;
}
}
/* 삭제할 노드를 못찾을 경우 */
if (!searched){
return false;
}
/*
* 위의 코드가 실행하면
* currNode 에는 삭제할 노드가 들어있다.
* currParentNode 에는 삭젤할 노드의 부모 노드가 들어있다.
*/
/* case 1: 삭제할 Node 가 Leaf 노드인 경우 */
if (currNode.left == null && currNode.right == null){
/* 부모 노드의 왼쪽에 있을 경우 */
if (currNode.value < currParentNode.value){
currParentNode.left = null;
}else {
/* 부모 노드의 오른쪽에 있을 경우 */
currParentNode.right = null;
}
return true;
/* case 2-1: 삭제할 Node 가 Child Node를 한 개 가지고 있을 경우(왼쪽에 Child Node) */
}else if (currNode.left != null && currNode.right == null){
/* 삭제할 노드가 부모 노드의 왼쪽에 있을 경우 */
if (value < currParentNode.value){
currParentNode.left = currNode.left;
}else {
/* 삭제할 노드가 부모 노드의 오른쪽에 있을 경우 */
currParentNode.right = currNode.left;
}
return true;
/* case 2-2: 삭제할 Node 가 Child Node를 한 개 가지고 있을 경우(오른쪽에 Child Node) */
}else if (currNode.left == null && currNode.right != null){
/* 삭제할 노드가 부모 노드의 왼쪽에 있을 경우 */
if (value < currParentNode.value){
currParentNode.left = currNode.right;
}else {
/* 삭제할 노드가 부모 노드의 오른쪽에 있을 경우 */
currParentNode.right = currNode.right;
}
return true;
/* Case 3-1: 삭제할 노드 가 자식 노드를 두 개 가지고 있을 경우 */
}else {
/* 삭제할 노드가 부모 노드의 왼쪽에 있을 때 */
if (value < currParentNode.value){
Node changeNode = currNode.right;
Node changeParentNode = currNode.right;
while (changeNode.left != null){
changeParentNode = changeNode;
changeNode = changeNode.left;
}
/* while 문이 돌고나면 changeNode 에는 삭제할 노드의 오른쪽 노드중 가장 작은 값의 노드가 들어있게 된다*/
/* Case 3-1-2 changeNode 의 오른쪽에 Child Node 가 있을 때 */
if (changeNode.right != null){
changeParentNode.left = changeNode.right;
/* Case 3-1-1 changeNode 의 오른쪽에 Child Node 가 없을 때 */
}else {
changeParentNode.left = null;
}
/* 삭제할 노드의 부모 노드에 연결해 준다. */
currParentNode.left = changeNode;
/* 삭제할 노드가 가지고있던 오른쪽 왼쪽 노드를 바꿀 노드에 연결해 준다. */
changeNode.left = currNode.left;
changeNode.right = currNode.right;
}else {
/* 삭제할 노드가 부모 노드의 오른쪽에 있을 때 */
Node changeNode = currNode.right;
Node changeParentNode = currNode.right;
while (changeNode.left != null){
changeParentNode = changeNode;
changeNode = changeNode.left;
}
/* while 문이 돌고나면 changeNode 에는 삭제할 노드의 오른쪽 노드중 가장 작은 값의 노드가 들어있게 된다*/
/* Case 3-2-2 changeNode 의 오른쪽에 Child Node 가 있을 때 */
if (changeNode.right != null){
changeParentNode.left = changeNode.right;
/* Case 3-2-1 changeNode 의 오른쪽에 Child Node 가 없을 때 */
}else {
changeParentNode.left = null;
}
/* 삭제할 노드의 부모 노드에 연결해 준다. */
currParentNode.right = changeNode;
/* 삭제할 노드가 가지고있던 오른쪽 왼쪽 노드를 바꿀 노드에 연결해 준다. */
changeNode.left = currNode.left;
changeNode.right = currNode.right;
}
}
}
return true;
}
}
public static void main(String[] args) {
// Case 3-1: 삭제할 노드가 자식 노드를 두 개 가지고 있을 경우
MyTree myTree = new MyTree();
myTree.addNode(10);
myTree.addNode(15);
myTree.addNode(13);
myTree.addNode(11);
myTree.addNode(14);
myTree.addNode(18);
myTree.addNode(16);
myTree.addNode(19);
myTree.addNode(17);
myTree.addNode(7);
myTree.addNode(8);
myTree.addNode(6);
System.out.println(myTree.delete(15));
System.out.println("ROOT: " + myTree.root.value);
System.out.println("ROOT LEFT: " + myTree.root.left.value);
System.out.println("ROOT LEFT LEFT: " + myTree.root.left.left.value);
System.out.println("ROOT LEFT RIGHT: " + myTree.root.left.right.value);
System.out.println("ROOT RIGHT: " + myTree.root.right.value);
System.out.println("ROOT RIGHT LEFT: " + myTree.root.right.left.value);
System.out.println("ROOT RIGHT RIGHT: " + myTree.root.right.right.value);
System.out.println("ROOT RIGHT RIGHT LEFT: " + myTree.root.right.right.left.value);
System.out.println("ROOT RIGHT RIGHT RIGHT: " + myTree.root.right.right.right.value);
}
실행 시키면 다음과 같이 나온다.
true
ROOT: 10
ROOT LEFT: 7
ROOT LEFT LEFT: 6
ROOT LEFT RIGHT: 8
ROOT RIGHT: 16
ROOT RIGHT LEFT: 13
ROOT RIGHT RIGHT: 18
ROOT RIGHT RIGHT LEFT: 17
ROOT RIGHT RIGHT RIGHT: 19
트리는 삭제할때 정말 복잡한것같다.
전체코드는 여기에서 확인하면 된다.
참조
https://st-lab.tistory.com/300
https://heung-bae-lee.github.io/2020/05/02/data_structure_06/
